Tutoriel CAN/CNA

Le monde actuel est encombré de signaux numériques et analogiques. Même si ces signaux se comportent différemment, ils sont souvent utilisés pour atteindre un objectif plus important. Imaginez un ingénieur chargé de contrôler une unité CVC. S'il envisage d'utiliser un microcontrôleur ou un microprocesseur, le dispositif devra pouvoir lire une température analogique qui présente un nombre infini de valeurs, et la convertir en représentation binaire configurée en étapes discrètes. Cette représentation binaire de la valeur analogique sera ensuite traitée par le microcontrôleur ou le microprocesseur. Ces données sont utilisées pour permettre à l'unité CVC d'exécuter un processus permettant de maintenir un environnement stable. Il est nécessaire d'utiliser un convertisseur analogique-numérique (CAN) pour transformer des valeurs analogiques qui doivent être traitées par un système numérique. La même théorie peut être appliquée dans le cas contraire pour un signal numérique qui nécessite d'être converti en un signal analogique. Diffuser une chanson en ligne implique de passer par plusieurs étapes pour convertir des signaux numériques en signaux analogiques. Le signal que le dispositif hôte reçoit en provenance du serveur correspond à une représentation binaire du signal analogique d'origine. La réponse audible de ces données binaires serait incompréhensible pour la personne qui l'écoute. Si le signal d'origine est un signal analogique, sa représentation finale devra obligatoirement être analogique. L'utilisation d'un convertisseur numérique-analogique (CNA) permet de résoudre ce problème. Ce type de dispositif traite du code binaire qui aurait pu être codé par un convertisseur analogique-numérique et permet de le transformer à nouveau en tension analogique.

Actuellement, la conversion de signaux analogiques en signaux numériques ou inversement est une tâche inévitable pour les ingénieurs. Il existe de nombreux types différents de convertisseurs analogique-numérique et numérique-analogique. Même s'ils présentent une architecture distincte, ils participent tous à l'accomplissement d'un objectif similaire. Tout comme il est impossible de traiter des signaux numériques avec des valeurs analogiques, cette situation est semblable à celle d'un Français essayant de discuter avec un Allemand. C'est impossible sans traducteur. Les CAN et CNA peuvent jouer le rôle d'un traducteur. Lorsqu'un CAN détecte une tension analogique, sa tâche consiste à convertir cette tension analogique en code binaire à un moment donné. Cela signifie que le CAN échantillonne la tension analogique à un instant, puis il détermine quelle serait la valeur en binaire sur le côté sortie du CAN. Le nombre d'échantillons pouvant être traités par le dispositif chaque seconde est indiqué dans sa documentation. Le MAX1118EKA+T de Maxim Integrated est un exemple. Ce dispositif présente une fréquence d'échantillonnage de 100 kHz, ce qui lui permet d'échantillonner la tension analogique entrante 100 000 fois par seconde. Grâce à sa capacité de traitement d'autant d'échantillons par seconde, il est possible d'enregistrer avec précision la représentation de la tension analogique à l'aide d'une interprétation binaire. Parfois, la fréquence d'échantillonnage d'un CAN n'est pas suffisante pour traduire précisément les données, ce qui provoque un repliement. Ce repliement empêche d'identifier les signaux les uns par rapport aux autres ou entraîne le recouvrement de ces signaux. Imaginez une caméra capable d'enregistrer 24 images par seconde. Pour la plupart des applications, cette fonctionnalité peut suffire, cependant si vous essayez de filmer quelque chose qui se déplace très rapidement, l'image pourrait être déformée. Souvenez-vous de l'effet produit lorsque vous voyiez un téléviseur sur un enregistrement à la fin des années 1990. L'image sur le téléviseur papillotait. Cela est dû au fait que la fréquence de rafraîchissement sur le téléviseur est bien plus rapide que ce que l'enregistrement peut capturer comme nombre d'images par seconde donné. L'image est déformée, car la vidéo consiste en une succession d'images. Il se produit plus de choses entre chaque image que ce qui est visible sur la vidéo. Le même type d'effet peut se produire avec un CAN. Pour éviter cela, il convient de s'assurer que la fréquence d'échantillonnage est au moins deux fois supérieure à la fréquence la plus élevée nécessaire à la transmission. Cela correspond au taux de Nyquist.

Une fréquence d'échantillonnage supérieure permettra au dispositif d'être plus précis, mais ce n'est pas l'unique paramètre permettant de contrôler la précision. Puisqu'il s'agit de la conversion d'un signal analogique en code binaire, il existe un nombre fini d'étapes discrètes pouvant être utilisées pour représenter la tension à un moment donné. Le nombre de bits pouvant être utilisés pour représenter ce nombre correspond à la résolution. Plus la résolution d'un CAN est élevée, plus il peut traiter de d'étapes discrètes. En outre, il est important de comprendre comment déterminer le nombre d'étapes qu'un CAN peut effectuer. La sortie binaire du CAN représente la tension d'alimentation. Si la tension d'alimentation est de 10 V avec un CAN 8 bits, la capacité est de 256 étapes. Pour calculer la résolution, utilisez l'équation 2ⁿ. Le « 2 » reste constant, tandis que le « N » correspond au nombre de bits. 2⁸ correspond à 256 étapes. L'utilisation de 256 étapes avec une tension de 10 V signifie que chaque étape est de 39,0625 mV. Le code binaire est différent pour chacune de ces étapes. Le relevé de toutes les options d'entrée possibles sur un CAN, du plus bas au plus haut, peut être représenté par un escalier. Cet escalier correspond à la fonction de transfert du CAN. La Figure 1 illustre le transfert à l'aide d'un CAN 3 bits avec une référence de 2 V.

Figure 1 : Fonction de transfert d'un CAN 3 bits avec référence de 2 V (avec l'autorisation de Microchip Technology).

Comme il s'agit de 3 bits, il est possible de calculer le nombre total d'étapes à l'aide de l'équation 2ⁿ comme suit :

Comme la Figure 1 le met en évidence, il existe 8 étapes entre 000 et 111. Chaque étape permet de déplacer d'un LSB vers le haut.

Comme indiqué précédemment, il existe différents types d'architectures CAN. Les trois architectures CAN les plus populaires sont les convertisseurs SAR (registre d'approximations successives), Delta-Sigma (∆∑) et pipeline. Chacune de ces architectures permet de convertir un signal analogique en sortie numérique, mais leurs traitements sont légèrement différents. Le convertisseur SAR échantillonne une entrée analogique et la retient, la transforme en signal numérique, puis transfère ce signal. Les convertisseurs Delta-Sigma traitent la valeur moyenne de l'échantillon sur la durée nécessaire pour la conversion de cet échantillon en signal numérique. Les convertisseurs à chevauchement (pipeline) répartissent la conversion entre plusieurs étages pour produire des vitesses de conversion très élevées. Chacune de ces architectures présente des aspects positifs et négatifs. L'architecture SAR est facile à utiliser, consomme généralement moins d'énergie et présente une faible latence ainsi qu'une extrême précision. L'architecture Sigma-Delta offre une très haute résolution et une très grande stabilité avec une faible consommation, à moindres frais ; cependant, elle fonctionne à des vitesses plus basses que les architectures SAR et pipeline. Le CAN pipeline fonctionne à des vitesses et une bande passante plus élevées que celles proposées par les exemples précédents, mais elle offre une résolution plus faible et consomme plus d'énergie.

Registres d'approximations successives

Les architectures à registres d'approximations successives sont les types de CAN les plus courants. Ces CAN sont généralement dotés d'une interface I²C ou SPI, mais ils peuvent également disposer d'une sortie parallèle. Pour faciliter la conversion du signal analogique, les CAN SAR comportent un échantillonneur pour tenter de maintenir un signal constant. Un comparateur permet de mesurer l'entrée analogique par rapport à un CNA interne. Le CNA sera défini sur la moitié de sa tension potentielle à ce point. Si l'entrée est supérieure à celle du CNA, le comparateur produit un 1 qui est stocké dans le MSB dans le registre d'approximations successives. Ensuite, le CNA est défini sur le quart de sa tension potentielle et le processus est réitéré. La valeur suivante du CNA est 1/8, puis 1/16 et ainsi de suite jusqu'au chargement de tous les bits dans le registre. Une comparaison permet d'illustrer ce processus qui implique d'ajouter successivement ou de ne pas ajouter des poids pour connaître le poids de quelque chose. La Figure 2 ci-dessous illustre cette théorie.

Figure 2 : Illustration d'un CAN à approximations successives pour obtenir une valeur numérique à partir d'une valeur analogique (avec l'autorisation d'Analog Devices).

Le bloc est constitué de 45 unités. Le premier test consiste à utiliser 32 petits blocs représentant chacun une unité de 1. Le bloc est toujours plus lourd que les petits blocs. Puisque le bloc est toujours plus lourd, les petits blocs restent en place. Le test suivant consiste à ajouter 16 petits blocs supplémentaires. Cela correspond à 32 + 16, ce qui équivaut à 48 et indique un poids trop lourd. Par conséquent, les 16 blocs sont mis de côté. Le test suivant consiste à ajouter 8 blocs supplémentaires à l'échelle, soit 32 + 8, ce qui donne pour résultat 40. Cette quantité est ajoutée. À partir de ce moment, il est possible d'ajouter 4 blocs supplémentaires, ce qui équivaut à 44 blocs. Deux blocs supplémentaires sont ensuite ajoutés, mais le résultat sera de 46 unités, ce qui est supérieur à 45. Les blocs sont donc retirés. Enfin, un bloc est ajouté pour que le poids des blocs soit identique de chaque côté. Chaque fois que des blocs ont été ajoutés, leur nombre a été divisé par deux. Cela est représentatif de la valeur donnée par le CNA sur le registre d'approximations successives. La Figure 3 présente un schéma fonctionnel d'un CAN à registre d'approximations successives.

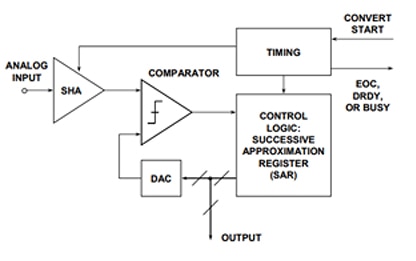
Figure 3 : Schéma fonctionnel d'un CAN à approximations successives (avec l'autorisation d'Analog Devices).

L'ADS7886SDBVT est un exemple de CAN SAR de Texas Instruments. Il s'agit d'un CAN 12 bits, ce qui signifie qu'il peut traiter 4096 étapes entre 0 V et la tension d'alimentation. La fréquence d'échantillonnage est de 1 MHz, ce qui signifie que le convertisseur vérifie l'entrée un million de fois par seconde. Comme les performances du CAN doivent être testées avant qu'il soit implémenté dans un produit fini, les fabricants créent souvent un outil d'évaluation pour faciliter les tests. L'ADS7886EVM est l'outil d'évaluation du convertisseur ADS7886SDBVT. Ces outils facilitent les tests, car il existe déjà une carte configurée avec tous les autres composants passifs nécessaires au test fonctionnel du CAN.

Sigma-Delta ∆∑

Les convertisseurs Sigma-Delta constituent un choix populaire lorsqu'une haute résolution et une haute précision sont nécessaires. L'enregistrement audio constitue un bon exemple d'une application avec un convertisseur Sigma-Delta. Les convertisseurs Sigma-Delta doivent suréchantillonner leurs entrées. Le taux de Nyquist n'est pas très pertinent lorsqu'il est question de convertisseurs Sigma-Delta. Ils fonctionnent de façon optimale lorsque la fréquence d'échantillonnage est environ 20 fois supérieure à la plus haute fréquence à échantillonner. La sortie du convertisseur Sigma-Delta est alimentée dans un filtre numérique et un décimateur traitant le flux binaire pour produire la sortie finale. Une interface série est souvent présente entre le filtre numérique et la sortie. L'AD7175-2BRUZ d'Analog Devices, Inc est un exemple de CAN Sigma-Delta. La Figure 4 illustre le schéma fonctionnel de l'AD7175-2BRUZ.

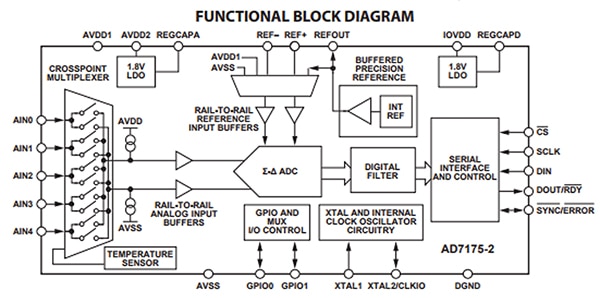
Figure 4 : Schéma fonctionnel du CAN Sigma-Delta AD7175-2BRUZ d'Analog Devices (avec l'autorisation d'Analog Devices).

Le CAN Sigma-Delta offre une résolution de 24 bits et une fréquence d'échantillonnage de 250 kHz. Il peut traiter jusqu'à 16 777 216 étapes. Cela signifie qu'il offre une résolution bien supérieure à celle du convertisseur de l'exemple précédent, cependant, environ ¼ de la fréquence d'échantillonnage. Comme dans l'exemple précédent, l'AD7175-2BRUZ est doté d'une carte d'évaluation à des fins de tests. Cette carte est l'EVAL-AD7175-2SDZ et permet d'évaluer facilement le CAN.

Pipeline

Les CAN à chevauchement (pipeline) sont les plus rapides. L'exemple tiré du tutoriel « ADC Architectures V: Pipelined Subranging ADCs » permet d'illustrer cette capacité avec un CAN à chevauchement de 6 bits. L'échantillonneur est similaire à celui des convertisseurs SAR, mais immédiatement après l'échantillonneur, un convertisseur Flash sous-CAN flash 3 bits numérise le signal. La conversion 3 bits est effectuée pour les 3 bits les plus significatifs. Ils sont convertis en signal analogique à l'aide d'un sous-CNA. Ce signal de sortie est soustrait à la sortie de l'échantillonneur, amplifié, puis renvoyé au sous-CAN 3 bits du deuxième étage pour les trois derniers bits les moins significatifs. La Figure 5 présente un schéma fonctionnel illustrant ce concept.

Figure 5 : Schéma fonctionnel d'un CAN pipeline (avec l'autorisation d'Analog Devices).

L'ADC10080CIMT est un exemple de CAN pipeline de Texas Instruments. Il s'agit d'un CAN 10 bits, il peut donc traiter 1 024 étapes et convertir 80 méga-échantillons par seconde. Ce dispositif peut être utilisé dans les applications d'ultrasons et d'imagerie, d'instrumentation, de systèmes d'acquisition de données ou dans toute application exigeant une conversion rapide. Le schéma fonctionnel de l'ADC10080CIMT/NOPB illustre la configuration, comme décrit ci-dessus. La Figure 6 correspond au schéma fonctionnel tiré de la fiche technique de l'ADC1008CIMT/NOPB.

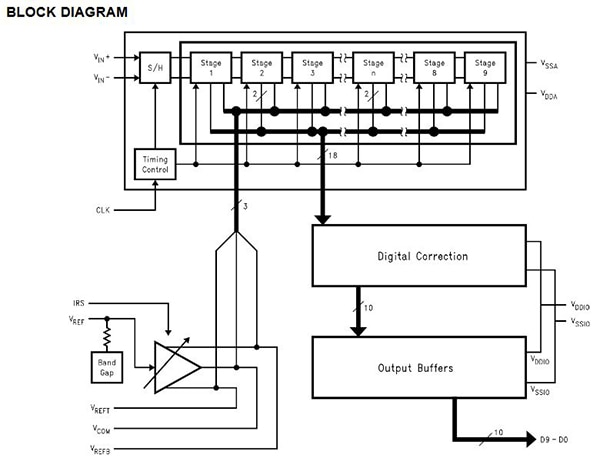
Figure 6 : Schéma fonctionnel de l'ADC10080CIMT/NOPB de Texas Instruments (avec l'autorisation de Texas Instruments).

CNA à pondération binaire

Jusqu'à maintenant, cet article s'est concentré sur la conversion de données par un CAN, mais ce n'est pas terminé. Il est souvent nécessaire de reconvertir des données binaires en signal analogique. C'est à ce moment que le convertisseur numérique-analogique intervient. Le premier type de CNA habituellement étudié en cours est le CNA à pondération binaire. Cela implique l'utilisation d'un système de résistances dont les sorties sont toutes reliées à la même résistance de sommation. Les bits les plus significatifs émettent plus de courant que les bits les moins significatifs. La création d'un réseau résistif inversement proportionnel permet de produire cette conversion. Étant donné que chaque bit binaire du code numérique a la même valeur de tension, en utilisant les résistances inversement proportionnelles sur chaque bit, les bits plus élevés permettent la circulation d'un flux de courant plus important. Cette méthode de conversion particulière est beaucoup moins utilisée actuellement au profit de méthodes plus simples ; cependant, elle constitue un très bon point de départ pour décrire le fonctionnement d'un CNA. La difficulté majeure soulevée par cette méthode consiste à trouver des résistances de niveaux différents qui peuvent fonctionner ensemble. La tolérance doit être extrêmement étroite et les résistances affichant des valeurs similaires sont plus courantes que les résistances avec des valeurs différentes, comme celles utilisées avec la méthode à pondération binaire. La Figure 7 illustre cette architecture à l'aide d'un schéma de réseau de résistances à pondération binaire.

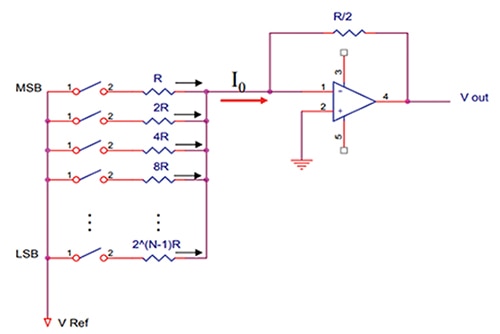
Figure 7 : Représentation schématique d'un réseau de registres à pondération binaire (avec l'autorisation de Georgia Institute of Technology).

CNA en chaîne

Les CNA en chaîne représentent un autre type d'architecture de CNA courant. C'est l'architecture la plus simple, mais également la moins linéaire. Elle est parfois appelée diviseur de Kelvin. Elle correspond à une chaîne de résistances de valeurs égales en série. La chaîne a une tension de référence en premier, une résistance à impédance élevée qui précède la chaîne et chaque nœud est doté d'un commutateur dédié au code binaire qui se ferme lorsque le code est lu par le dispositif. Cela permet d'utiliser une valeur de tension analogique dépendante de l'entrée binaire. La Figure 8 est tirée d'une vidéo intitulée « What is a String DAC? » de Texas Instruments. Le code 010 est défini pour la valeur décimale de 2. Le commutateur à 010 est maintenant fermé, ce qui permet à la tension CC à ce nœud de circuler vers l'amplificateur de sommation.

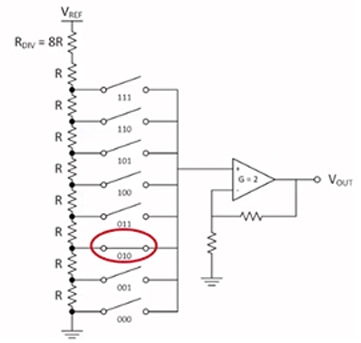
Figure 8 : Représentation schématique d'un CNA en chaîne (avec l'autorisation de Texas Instruments).

Il est facile de produire des CNA en chaîne, car des valeurs de résistance identiques sont utilisées pour chaque portion de la chaîne (à l'exception de la résistance à impédance élevée). L'AD5683RBRMZ est un exemple de CNA en chaîne d'Analog Devices Inc. Il s'agit d'un CNA en chaîne 16 bits fonctionnant avec une interface SPI. La Figure 9 montre le schéma fonctionnel de ce dispositif et la Figure 10 illustre le diviseur résistif. Ce produit possède également un outil d'évaluation, l'EVAL-AD5683RSDZ.

Figures 9 et 10 : Schéma fonctionnel de l'AD5683RBRMZ d'Analog Devices (à gauche) et de son réseau de diviseur résistif (à droite) (avec l'autorisation d'Analog Devices).

R-2R

Le réseau R-2R constitue une architecture très courante de CNA. Cette architecture n'utilise que deux valeurs de résistances. Les valeurs ne sont pas importantes tant que 2R est deux fois supérieure à R. Cela rend les CNA R-2R très polyvalents. Quelle que soit la résolution du CNA, des résistances de deux valeurs sont nécessaires. La Figure 11 illustre un réseau en échelle R-2R 4 bits.

Figure 11 : Représentation schématique d'un CNA R-2R (avec l'autorisation d'Analog Devices).

Ce réseau diviseur applique le théorème de Thévenin pour obtenir la résistance équivalente de Thévenin pour l'ensemble du réseau de « R ». Chaque étage permet de doubler la tension en tant que dernier étage. Dans cet exemple, si Vref est de 5 V, alors l'étage le plus à gauche pour le bit le moins significatif peut seulement produire 0,3125 V. En allant de gauche à droite, la tension de sortie proportionnelle serait comme suit :

Cela est représentatif de toutes les entrées numériques, X0 correspondant au bit le moins significatif et X3 au bit le plus significatif. En utilisant une tension de référence de 5 V, le résultat serait le suivant :

En conservant la même logique, pour trouver la tension analogique du bit le plus significatif, il est possible d'établir l'équation suivante :

Si l'entrée binaire était 1111, la sortie n'équivaudrait pas à 5 V. Souvenez-vous de l'explication sur la résolution abordée précédemment. S'il s'agit d'un CNA 4 bits, il peut traiter 16 étapes. En effet, 2⁴ correspond à 16 étapes. Le bit le moins significatif est à 0,3125 V. En multipliant 0,3125 par 16, le résultat obtenu est 5. C'est trompeur, car l'une des étapes implique un seuil de 0 V pour représenter 0000 binaire. Cela signifie que la tension la plus élevée pouvant être atteinte est la tension d'alimentation moins la tension de l'un des bits les moins significatifs. Ce qui donne pour résultat 4,6875 V.

Le DAC8734SPFB est un exemple de CNA R-2R de Texas Instruments. Il s'agit d'un convertisseur 16 bits qui montre à quel point ces dispositifs sont évolutifs. La configuration utilisée pour le réseau R-2R est très similaire à celle décrite ci-dessus. La Figure 12 illustre le réseau R-2R du DAC8734SPFB. Un outil d'évaluation est également disponible avec le DAC8734SPFB, le DAC8734EVM.

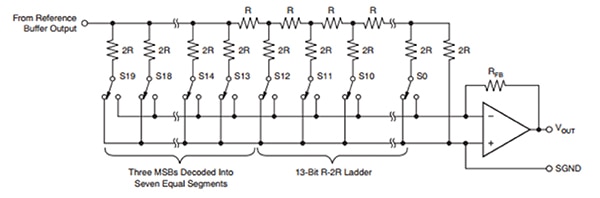
Figure 12 : Représentation schématique du CNA R-2R DAC8734SPFB de Texas Instruments (avec l'autorisation de Texas Instruments).

Il existe beaucoup d'autres architectures de CAN ou de CNA, mais cet article ne couvre que certaines des architectures les plus courantes. Ces dispositifs sont nécessaires dans le monde actuel du traitement numérique des signaux. Sans les convertisseurs CAN/CNA, il serait impossible d'intégrer une sortie analogique dans tout type de traitement numérique des signaux ou inversement. Il est possible que cette conversion coule de source pour le profane, mais pour l'ingénieur chargé de connecter des composants analogiques à un système numérique, c'est l'une des étapes les plus importantes à prendre en considération. Lorsque vous pensez à la conversion analogique-numérique, souvenez-vous de la comparaison représentant deux personnes qui parlent deux langues différentes. Si un traducteur n'est pas présent, ces deux personnes ne seront pas capables de communiquer. Sans l'utilisation de convertisseurs CAN ou CNA adéquats, un dispositif devrait utiliser uniquement des signaux analogiques ou uniquement des signaux numériques. Les convertisseurs CAN/CNA constituent une excellente liaison entre ces deux mondes.

Ressources

1. “AVR127: Understanding ADC Parameters”. Mai 2016
2. “Choose the right A/D converter for your application”. Extrait daté du 8 mai 2017.
3. Kester, Walt. “ADC Architectures II: Successive Approximation ADCs”. Octobre 2008.
4. Kester, Walt. “ADC Architectures III: Sigma-Delta ADC Basics”. Octobre 2008.
5. Kester, Walt. “ADC Architectures IV: Sigma-Delta ADC Advanced Concepts and Applications”. Octobre 2008.
6. Kester, Walt. “ADC Architectures V: Pipelined Subranging ADCs” Oct. 2008.
7. Kester, Walt. “DAC Interface Fundamentals”. Octobre 2008.
8. Kester, Walt. “Basic DAC Architectures II: Binary DACs”. Octobre 2008.
9. Lee, J., Jeelani K., Beckwith, J. “Digital to Analog Converter”. Extrait daté du 8 mai 2017
10. Poole, Matt. “What is a String DAC?”. 4 avril 2016