Concevoir une combinaison fiable et précise de circuit d'attaque d'amplificateur opérationnel et de CAN SAR pour une imagerie médicale de précision

Les applications d'imagerie médicale telles que l'imagerie par résonance magnétique (IRM), les échographes et les appareils à rayons X dépendent de quantités croissantes de données précises, surtout maintenant que les dispositifs et les systèmes sont de plus en plus connectés. Cependant, la précision des données dépend de la bonne conception du circuit d'entrée pour acquérir le signal du capteur, tout en minimisant l'instabilité due au bruit avant la conversion du signal détecté vers le domaine numérique.

Le problème de la stabilité est en partie résolu en utilisant un convertisseur analogique-numérique (CAN) à registre d'approximations successives (SAR) à entrée différentielle afin de fournir des résultats numériques précis pour un signal d'entrée analogique donné. Cependant, si le signal d'entrée est instable à cause du bruit, le convertisseur peut uniquement produire fidèlement le bruit du signal d'entrée. Le défi consiste à faire en sorte que le bruit du système analogique et la largeur de bande de l'amplificateur opérationnel complètent le CAN SAR.

Cet article traite brièvement de la sélection appropriée de l'amplificateur opérationnel complémentaire et du CAN SAR haute résolution. Il présente ensuite un CAN SAR et un amplificateur entièrement différentiel d'Analog Devices, et montre comment les combiner pour atteindre des performances de distorsion harmonique totale (THD) et de rapport signal/bruit (SNR) 16 bits.

Exigences de performances d'imagerie médicale

Lorsque vous travaillez avec un équipement médical d'imagerie, chaque résultat de sortie a un impact considérable sur la capacité du médecin à évaluer et à prescrire des traitements efficaces. Que l'équipement médical soit une unité IRM, un échographe ou un appareil à rayons X, les résultats de l'équipement et l'évaluation du médecin peuvent permettre de faire basculer le processus des symptômes vers une action raisonnable. Un équipement médical hautes performances améliore la qualité de l'image et les résultats de sortie. Une amélioration de la sensibilité de l'équipement réduit l'exposition du patient et les tests répétitifs inutiles, et améliore la qualité de l'image de diagnostic.

Au niveau des composants, les amplificateurs de l'équipement, les CAN et leur implémentation définissent le niveau ultime de sensibilité et de qualité de l'image. Ces systèmes requièrent des performances 16 bits pour le processus de conversion analogique-numérique afin de garantir le maintien de la qualité de l'image au niveau de la sortie. En tant que point de départ pour les systèmes analogiques et numériques, cette résolution de 16 bits se traduit par des performances système typiques de SNR > 98 dB et de THD < -107,5.

Le rapport signal/bruit décrit la quantité de bruit qui passe sur un signal. Le rapport signal/bruit exclut les signaux harmoniques et le courant continu. Le rapport signal/bruit idéal pour un CAN SAR avec une entrée d'onde sinusoïdale pleine échelle est de (6,02 x n) +1,76 dB, n étant le nombre de bits du convertisseur. La distorsion harmonique totale est la somme efficace des puissances des composantes harmoniques (parasites) correspondant à un multiple du signal d'entrée, rapportée à la puissance du signal d'entrée. Ce rapport est spécifié en décibels (dB) efficaces.

Les performances requises peuvent être atteintes à l'aide de l'amplificateur opérationnel ADA4945-1ACPZ-R2 et le CAN SAR AD4003BCPZ-RL7 d'Analog Devices (Figure 1). L'ADA4945-1ACPZ-R2 est un amplificateur opérationnel haute vitesse, entièrement différentiel et à faible bruit dans une configuration gain unité. Il permet de commander efficacement les CAN SAR haute résolution. Il fonctionne sur une plage d'alimentation étendue (de 3 V à 10 V) et présente une faible tension de décalage ainsi qu'un faible bruit de 1,8 nV√Hz à 100 kHz. L'AD4003BCPZ-RL7 est un CAN SAR à entrée différentielle 18 bits, 2 Méch./s, avec un rapport signal/bruit typique égal à 100,5 dB, une distorsion harmonique totale de -123 dB et une non-linéarité intégrale (INL) de ±1,0 LSB (bit le moins significatif).

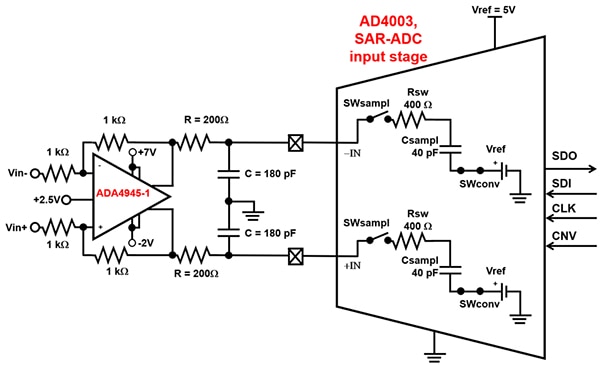Figure 1 : Circuit d'acquisition de données d'imagerie médicale simplifié basé sur l'amplificateur opérationnel ADA4945-1ACPZ-R2 et un CAN SAR AD4003BCPZ-RL7 d'Analog Devices. (Source de l'image : Bonnie Baker)

Analyse du bruit système

Un objectif clé de la conception des systèmes médicaux de précision consiste à atteindre un rapport signal/bruit élevé. Le moyen d'améliorer le rapport signal/bruit consiste à sélectionner des composants à faible bruit et à augmenter l'amplitude du signal pleine échelle (Figure 2).

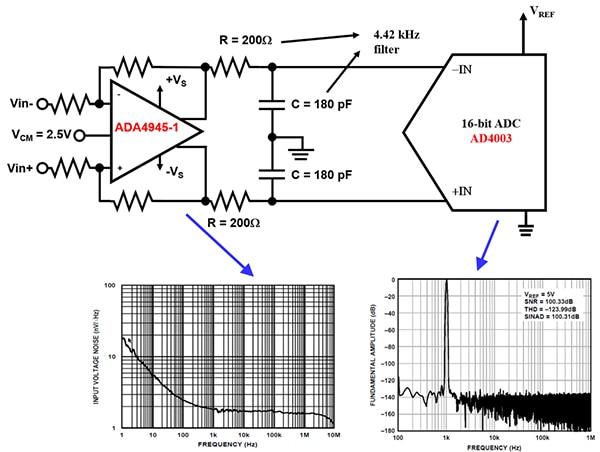Figure 2 : Les unités pour les spécifications de bruit dans le domaine analogique sont exprimées en temps et en fréquence. Les unités pour les spécifications de bruit dans le domaine numérique sont exprimées en dB. (Source de l'image : Bonnie Baker, selon un document d'Analog Devices)

Sur la Figure 1, l'alimentation de l'amplificateur ADA4945-1 est suffisamment étendue pour garantir des performances de sortie rail-à-rail sans distorsion. La référence 5 V du CAN SAR AD4003 couvre la plage d'entrée. La clé pour choisir les bons composants est de comprendre la puissance de bruit totale des composants de la chaîne de signaux.

Notez que les tracés inférieurs de la Figure 2 ont des unités différentes. Dans le domaine analogique, les unités de mesure du bruit sont exprimées en V/√Hz. Le bruit dans le domaine numérique est mesuré en dB. Comme indiqué, les unités de spécification de bruit entre les domaines analogique et numérique diffèrent.

Bruit d'un amplificateur opérationnel

Dans le domaine analogique, les unités de mesure du bruit sont également exprimées en volts efficaces pour une moyenne statistique sur une largeur de bande donnée. Par exemple, la tension de bruit d'entrée différentielle de l'ADA4945-1 est de 5 nV/√Hz à 5 Hz et de 1,8 nV/√Hz à 100 kHz (Figure 3).

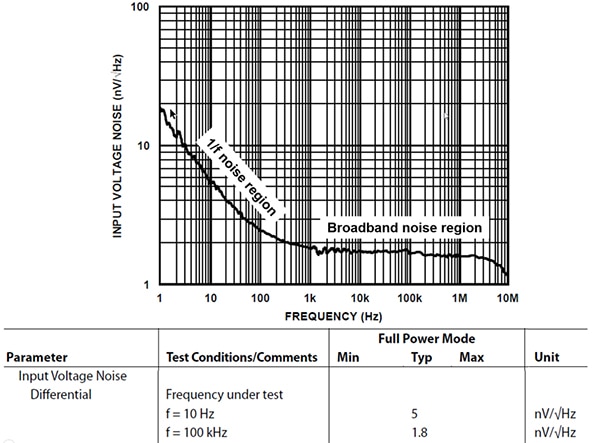Figure 3 : Tracé de la fréquence par rapport à la tension de bruit d'entrée de l'amplificateur ADA4945-1 illustrant les régions de bruit en 1/f et large bande de l'amplificateur. (Source de l'image : Bonnie Baker, selon un document d'Analog Devices)

Dans la Figure 3, le défi en ce qui concerne les deux régions de bruit consiste à les combiner en une moyenne statistique du bruit. Le bruit efficace de la région en 1/f référée à l'entrée peut être déterminé à l'aide de l'Équation 1 :

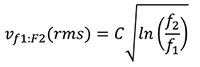Équation 1

Où C correspond à la densité de bruit de l'amplificateur à 1 Hz et f₁ et f₂ définissent la largeur de bande de la région en 1/f. Habituellement, f₁ est égale à 0,1 Hz.

Voici les chiffres :

f₁ = 0,1 Hz

f₂ = 1 kHz

C = 19 nV/√Hz

Le bruit efficace de l'ADA4945-1 dans la région en 1/f est de 57,66 nV efficaces

Le bruit efficace large bande de l'ADA4945-1 référé à l'entrée est calculé à l'aide de l'Équation 2 :

Équation 2

Où e_n correspond au bruit spécifié à une fréquence donnée dans la région large bande de l'amplificateur, et BW est la largeur de bande de la région large bande.

Avec :

e_n = 1,8 nV/√Hz

BW = 1 kHz à 4,42 MHz (remarque : avec filtre passe-bas de 200 ohms (W), 180 pF entre l'amplificateur opérationnel et le CAN)

Le bruit efficace dans la région large bande est de 4,74 mV efficaces.

La puissance totale de bruit présente dans tout système est égale à la valeur résultante quadratique (RSS) de la puissance de bruit fournie par ses parties de composantes individuelles. Le bruit total de l'amplificateur référé à l'entrée est calculé à l'aide de l'Équation 3 :

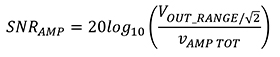Équation 3

Où G_AMP est égal au gain de l'amplificateur.

Avec G_AMP = 1, le bruit efficace total référé à la sortie de l'ADA4451 est de 4,74 mV efficaces.

Les unités de calcul du domaine analogique pour les équations 1, 2 et 3 sont la tension et la fréquence. La conversion de la tension analogique en une représentation en dB en tant que SNR est égale à SNR_AMP, comme indiqué dans l'Équation 4.

Équation 4

Où V_{OUT_RANGE} correspond à la plage d'entrée du CAN SAR.

Avec :

V_{OUT_RANGE} = 9,5 V

La valeur SNR_AMP de l'ADA4451-2, référée à sa sortie, est de +123 dB.

Distorsion de l'amplificateur

L'ADA4945-1 est fabriqué à l'aide du processus bipolaire complémentaire au silicium-germanium (SiGe) exclusif d'Analog Devices, qui permet d'obtenir de faibles niveaux de distorsion.

Avec une plage de tensions d'entrée de -V_S à (+V_S – 1,3 V), la distorsion par harmonique 2 (HD2) est égale à -133 décibels par rapport à la fréquence porteuse (dBc). HD2 et HD3 (distorsion par harmonique 3) correspondent à -140 dBc HD3 à 1 kHz. À 100 kHz, HD2 est égale à -133 dBc et HD3 est de -116 dBc.

Bruit d'un CAN SAR

La dérivation du bruit référé en entrée pour un amplificateur provient de deux points de mesure de fréquence (1 Hz et 100 kHz). La dérivation du rapport signal/bruit d'un CAN SAR est obtenue à l'aide d'un calcul RSS FFT et est exprimée en dB.

Le rapport signal/bruit idéal d'un CAN SAR est égal à (N x 6,02 + 1,76) dB, N étant égal au nombre de bits du convertisseur. Le CAN SAR ADA4003 est spécifié en tant que convertisseur 18 bits, ainsi le rapport signal/bruit idéal de ce convertisseur est égal à 110 dB. Toutefois, comme indiqué ci-après, le rapport signal/bruit réel de ce dispositif est égal à 100,3 dB.

Le spectre de fréquences de la mesure FFT du CAN SAR couvre de 0 à fs/2, où fs est égale à la fréquence d'échantillonnage des convertisseurs (Figure 4).

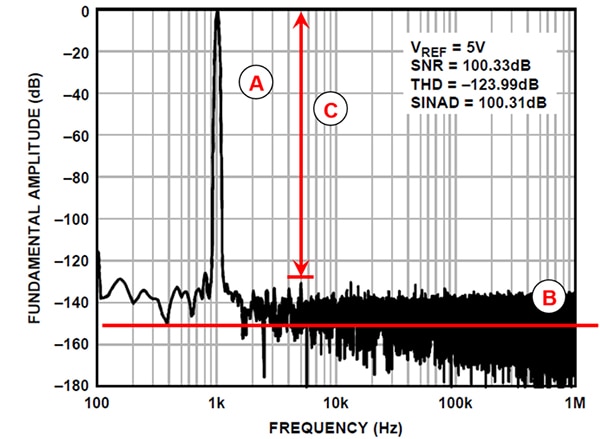Figure 4 : Le tracé de données FFT de l'ADA4003 permet de calculer le rapport signal/bruit et la distorsion harmonique totale d'un CAN. (Source de l'image : Bonnie Baker)

Dans la Figure 4, le parasite dominant (A) est le signal d'entrée du convertisseur. La ligne (B) montre le bruit de sortie du convertisseur, qui inclut la quantification et le bruit du composant interne. Le parasite secondaire (C), qui semble être HD5, représente la distorsion dominante à environ -128 dB. Tous les autres parasites dont les fréquences sont des multiples du signal d'entrée (A) sont ajoutés avec une formule RSS pour générer la valeur THD totale.

Combinaison SNR et THD : SINAD

Un facteur de mérite (FoM) à explorer est le rapport signal/bruit plus distorsion (SINAD ou SNR+D). Ce terme peut aussi être THD+bruit. La valeur SINAD est la combinaison calculée du rapport signal/bruit et de la distorsion harmonique totale, ou le rapport entre l'amplitude efficace du signal d'entrée fondamental et la somme efficace de toutes les autres composantes spectrales situées au-dessous de la moitié de la fréquence d'échantillonnage (à l'exclusion de CC). Le minimum théorique pour SINAD est égal au rapport signal/bruit idéal, soit 6,02n + 1,76 dB avec les convertisseurs à approximations successives et pipeline.

La valeur SINAD est exprimée en dBc lorsque la puissance absolue de la fondamentale est utilisée comme référence ou en décibels par rapport à la pleine échelle (dBFS) lorsque la puissance de la fondamentale est extrapolée à la plage pleine échelle du convertisseur.

La valeur SINAD est une spécification essentielle dans la conception des enregistreurs de formes d'ondes/oscilloscopes numériques, ainsi que dans les applications de traitement d'images géophysiques, de radar, de sonar, d'analyse de spectre, de télécommunications vidéo et de récepteur numérique large bande.

Bruit et distorsion combinés

Pour revenir à la conception d'origine, la configuration système requise est celle d'un système 16 bits. Cette résolution de 16 bits se traduit par des performances système typiques de rapport signal/bruit > 98 dB et de distorsion harmonique totale < -107,5.

Il est maintenant temps de combiner toutes les erreurs SNR et THD de l'amplificateur et celles du CAN SAR dans un seul facteur de mérite. Le bruit de l'amplificateur et celui du CAN SAR sont combinés pour déterminer le bruit total du système à l'aide de l'Équation 5 :

Équation 5

Dans l'Équation 5, les deux termes SNR avec des unités de dB ne peuvent pas être additionnés. Les termes SNR du CAN SAR et de l'amplificateur sont convertis en un rapport linéaire. Une fois cette opération terminée, ces termes sont additionnés, puis redéfinis en décibels.

La distorsion de l'amplificateur et celle du CAN SAR sont combinées pour déterminer la distorsion totale du système à l'aide de l'Équation 6 :

Équation 6

Le rapport signal/bruit du système est combiné à la distorsion harmonique totale du système à l'aide de l'Équation 7 :

Équation 7

Aux fréquences de signal de 1 kHz et 10 kHz, le rapport signal/bruit et la distorsion harmonique totale testés pour la combinaison de l'amplificateur ADA1945-1 qui commande le CAN SAR AD4003 répondent aux conditions requises de rapport signal/bruit > 98 dB et de distorsion harmonique totale < -107,5 (Tableau 1).

Tableau 1 : Synthèse des dispositifs ADA4945-1 et AD4003 selon la Figure 1. À 100 kHz, l'ADA4945-1 peut maintenir des performances de 16 bits, là où le rapport signal/bruit et la distorsion harmonique totale de l'AD4003 commencent à se dégrader. (Source du tableau : Bonnie Baker)

À 100 kHz, l'ADA4945-1 peut maintenir des performances de 16 bits, là où le rapport signal/bruit et la distorsion harmonique totale de l'AD4003 commencent à se dégrader.

Conclusion

La combinaison d'un amplificateur entièrement différentiel et d'un CAN SAR 18 bits est nécessaire pour créer un système 16 bits haute précision destiné aux unités IRM, aux échographes et aux systèmes à rayons X. Pour offrir les meilleures performances globales, les dispositifs ADA4945-1 et AD4003 d'Analog Devices constituent un bon choix pour offrir une solution à faible bruit et faible distorsion aux systèmes d'instrumentation médicale.