Initiation au traitement des signaux : filtre à moyenne mobile

Les signaux et les systèmes sont de puissants concepts en électrotechnique. Ils nous permettent de modéliser la manière dont les informations traversent les composants électriques et sont modifiées. De plus, une fois que nous avons compris comment les signaux tels que les tensions sont affectés par les différents composants électriques, nous pouvons concevoir des circuits pour manipuler les signaux comme nous le souhaitons. Il est donc fascinant de voir comment nous pouvons utiliser une combinaison de composants électriques, tels que des résistances, des condensateurs et des amplificateurs opérationnels, pour modéliser des outils mathématiques comme l'intégration et la différenciation.

Examinons par exemple le circuit suivant (Figure 1) :

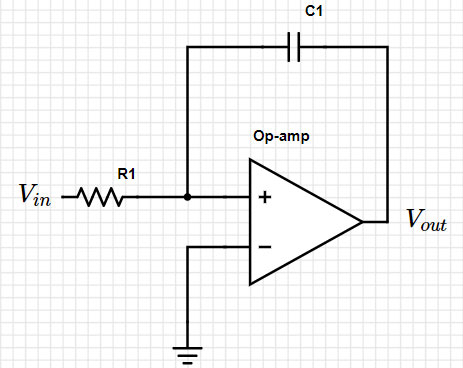Figure 1 : Circuit d'intégrateur simple. (Source de l'image : Mustahsin Zarif)

En passant dans le domaine de Laplace, nous pouvons représenter le circuit avec la formule suivante :

Vout = -(1/s) (1/RC) Vin

1/s dans le domaine de Laplace correspond en fait à une intégration. Nous disposons donc d'un modèle de circuit pour un circuit intégrateur utilisant un amplificateur opérationnel. Cependant, en pratique, les systèmes sont toujours contaminés par une forme ou une autre de bruit aléatoire.

Laissons de côté le circuit intégrateur pour un exemple plus simple : considérons un circuit amplificateur de tension dont les formes d'ondes d'entrée et de sortie peuvent être mesurées à l'aide d'un oscilloscope comme illustré à la Figure 2.

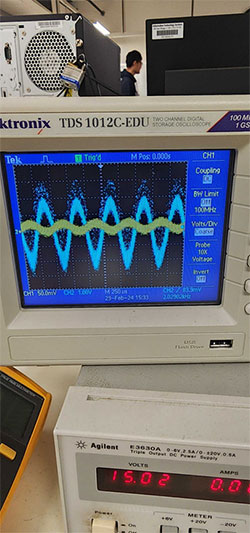Figure 2 : Formes d'ondes d'entrée et de sortie d'un amplificateur de tension. (Source de l'image : Mustahsin Zarif)

Le bruit aléatoire qui s'ajoute aux formes d'ondes sinusoïdales visibles sous-jacentes peut être dû à une pléthore de facteurs, tels que de mauvaises connexions électriques, le circuit étant construit sur un montage d'essai. Ce bruit affecte également la forme d'onde de l'intégrateur, problème que nous aborderons dans un prochain blog de cette série sur le traitement des signaux. Cependant, ce qui nous intéresse souvent, c'est de savoir comment minimiser les perturbations aléatoires.

Techniques de filtrage

Les ingénieurs préfèrent surmonter ces obstacles en utilisant des techniques de filtrage, que l'on peut classer comme suit : 1) filtres à réponse impulsionnelle finie (RIF) ou 2) filtres à réponse impulsionnelle infinie (RII).

Les filtres RIF sont appelés ainsi parce que la sortie à tout moment ne dépend que des valeurs actuelles et précédentes de l'entrée, et parce qu'ils ne dépendent pas des valeurs passées de la sortie. Ils présentent donc une structure non récursive sans rétroaction qui peut être modélisée comme dans l'Équation 1.

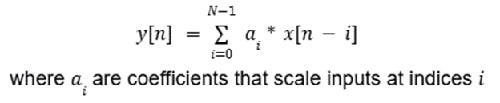Équation 1 : Exemple d'équation de filtre RIF. (Source de l'image : Mustahsin Zarif)

Le circuit intégrateur est un exemple de filtre RIF, car la sortie ne dépend que de l'entrée.

Les filtres RII, quant à eux, présentent une rétroaction, puisque la sortie à tout moment dépend des sorties précédentes ainsi que de l'entrée actuelle. Cela est modélisé par l'Équation 2.

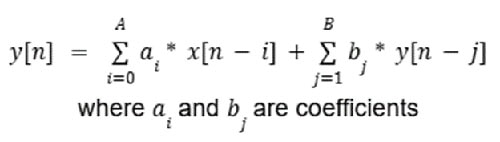Équation 2 : Exemple d'équation de filtre RII. (Source de l'image : Mustahsin Zarif)

La Figure 3 est la représentation visuelle du schéma fonctionnel d'un filtre RII, qui montre comment les entrées et les sorties sont retardées (z-i, z-j), mises à l'échelle (ai, bj) et additionnées pour donner la sortie actuelle. En modifiant ces valeurs, nous pouvons mettre en œuvre différents types de filtres.

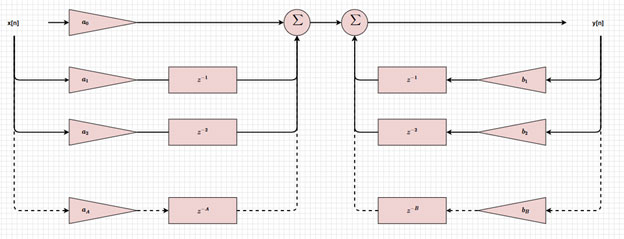Figure 3 : Schéma fonctionnel d'un filtre RII. (Source de l'image : Mustahsin Zarif)

Pour le schéma fonctionnel d'un filtre RIF sans rétroaction, y[n] serait simplement le résultat de la première sommation (Figure 4).

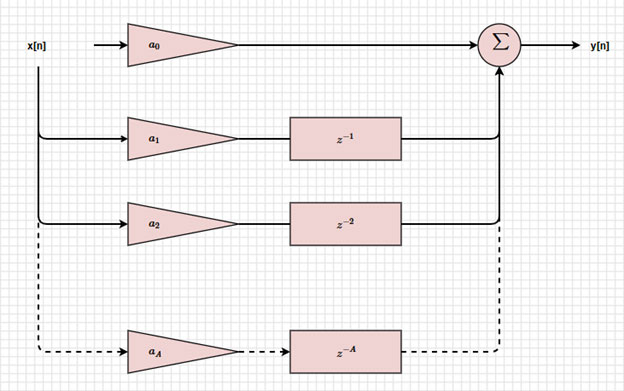Figure 4 : Schéma fonctionnel d'un filtre RIF. (Source de l'image : Mustahsin Zarif)

Maintenant que nous avons assimilé les bases des filtres RIF et RII, utilisons un exemple pour illustrer ce que nous avons appris : le filtre à moyenne mobile.

Le fonctionnement de la moyenne mobile consiste à prendre la moyenne de l'entrée actuelle et d'un certain nombre d'entrées précédentes (Équation 3).

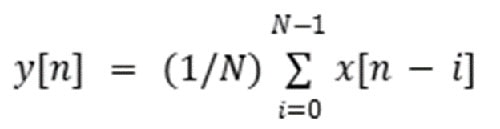Équation 3 : Équation de la moyenne mobile. (Source de l'image : Mustahsin Zarif)

Où N = taille de la fenêtre/nombre d'échantillons contribuant à la sortie

Nous pouvons voir qu'il s'agit d'un filtre RIF, puisqu'il n'y a pas de termes y du côté droit de l'équation.

Cependant, nous pouvons être astucieux et réorganiser l'équation pour former un filtre RII. Considérons l'exemple suivant :

Soit N=5, donc

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1])/5,

et y[6] = (x[6]+x[5]+x[4]+x[3]+x[2])/5

y[6]=(x[6]+y[5]-x[1])/5

Par conséquent, la sortie actuelle dépend maintenant de la sortie précédente (y[6] dépend de y[5]) !

Plus généralement,

y[n] = (y[n − 1] + x[n] − x[n − N - 1])/N

Où N = taille de la fenêtre

Ce filtre est particulièrement efficace pour le lissage des signaux du domaine temporel, comme illustré à la Figure 5, simulée avec Python pour une taille de fenêtre N = 11.

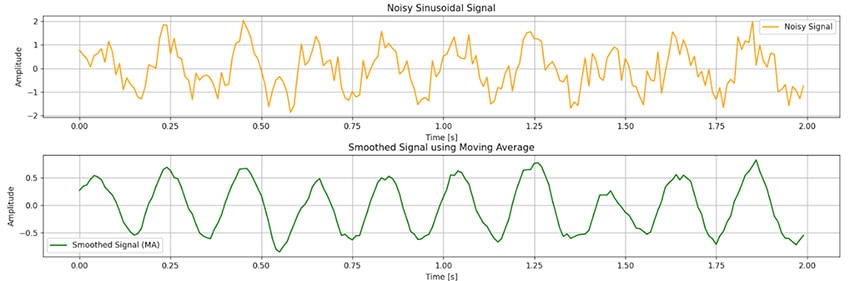Figure 5 : Simulation d'un filtre mobile avec Python. (Source de l'image : Mustahsin Zarif)

Code Python de simulation de filtre mobile :

Copieimport numpy as np

import matplotlib.pyplot as plt



# Parameters for the sinusoidal wave

frequency = 5  # in Hertz

sampling_rate = 100  # Sampling rate in samples per second

duration = 2  # in seconds



# Generate time axis

t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)



# Generate a clean sinusoidal signal

clean_signal = np.sin(2  np.pi  frequency * t)



# Add random, white (Gaussian) noise to the signal

noise_amplitude = 0.5

noisy_signal = clean_signal + noise_amplitude * np.random.normal(size=t.shape)



def moving_average(signal, window_size):

    window = np.ones(window_size) / window_size

    return np.convolve(signal, window, mode='same') 



# Apply moving average to the noisy signal

window_size = 11

smoothed_signal_ma = moving_average(noisy_signal, window_size)



# Plot the noisy and smoothed signals

plt.figure(figsize=(12, 9))



plt.subplot(2, 1, 1)

plt.plot(t, noisy_signal, label='Noisy Signal', color='orange')

plt.title('Noisy Sinusoidal Signal')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.subplot(2, 1, 2)

plt.plot(t, smoothed_signal_ma, label='Smoothed Signal (MA)', color='green')

plt.title('Smoothed Signal using Moving Average')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.tight_layout()

plt.show()

Résumé

Cet article de blog a montré comment, dans le monde réel, les données sont corrompues par le bruit. Bien que nous ne puissions pas obtenir la réponse idéale attendue des équations mathématiques, il est possible de filtrer les caractéristiques indésirables de nos données collectées afin de s'approcher autant que possible de la réponse idéale. Il existe plusieurs méthodes pour y parvenir et plusieurs scénarios dans lesquels nous voudrions le faire. Cet article a également présenté la réponse simulée d'un filtre à moyenne mobile. Dans le prochain article de blog, nous verrons comment le filtre à moyenne mobile exponentielle peut lisser les données d'unités de mesure inertielle (IMU) bruyantes.