Tutorial zu ADCs/DACs

Die Welt von heute ist von digitalen und analogen Signalen regelrecht übersät. Obwohl sich diese Signale von ihrem Verhalten her unterscheiden, werden häufig beide gemeinsam genutzt, um ein größeres Ziel zu erreichen. Nehmen Sie beispielsweise den Ingenieur, der mit der Steuerung eines HLK-Systems betraut wird. Wenn Mikrocontroller oder Mikroprozessoren verwendet werden sollen, ist es erforderlich, dass eine analoge Temperatur mit einer unendlichen Anzahl an Werten gelesen und in eine binäre Darstellung in diskreten Stufen gewandelt werden kann. Diese binäre Darstellung des analogen Werts wird dann vom Mikrocontroller oder Mikroprozessor verarbeitet. Diese Daten werden zur Ausführung eines Prozesses durch das HLK-System verwendet, um für gleichbleibende Umgebungsbedingungen zu sorgen. Wenn ein analoger Wert von einem digitalen System verarbeitet werden muss, ist ein Analog-Digital-Wandler (ADC) unerlässlich. Selbiges gilt auch für ein digitales Signal, das in ein analoges Signal gewandelt werden muss. Das Online-Streaming eines Musiktitels umfasst einige Schritte, bei denen digitale in analoge Signale gewandelt werden. Das Signal, das vom Server an das Host-Gerät übermittelt wird, ist eine binäre Darstellung des ursprünglichen Analogsignals. Die hörbare Antwort aus diesen binären Daten wäre für den Hörer nicht zu verstehen. Da es sich beim ursprünglichen Signal um ein analoges Signal gehandelt hat, muss auch die finale Darstellung dieses Signals analog sein. Dieses Problem kann durch einen Digital-Analog-Wandler (DAC) behoben werden. Mit dieser Komponente kann binärer Code, der mit einem ADC verschlüsselt wurde, wieder in eine analoge Spannung umgewandelt werden.

Die Wandlung analoger in digitale oder digitaler in analoge Signale ist für Ingenieure heutzutage unvermeidbar. Es gibt viele verschiedene Arten von Analog-Digital- und Digital-Analog-Wandlern. Diese unterscheiden sich zwar hinsichtlich ihrer Architektur, haben aber alle eine ähnliche Aufgabe zu erfüllen. Analoge Werte sind für die digitale Signalverarbeitung ungeeignet. Analog dazu könnte man versuchen, sich mit jemandem auf Französisch zu unterhalten, der diese Sprache nicht versteht. Ohne Übersetzer hätte das keinen Sinn. ADC- und DAC-Komponenten fungieren als eine Art Übersetzer. Ein ADC hat die Aufgabe, eine analoge Spannung zu einem bestimmten Zeitpunkt in einen Binärcode umzuwandeln. Das bedeutet, dass der ADC die analoge Spannung abtastet und anschließend ermittelt, welcher binäre Wert sich am Ausgang des ADC ergibt. Die von der Komponente durchgeführte Anzahl an Abtastungen pro Sekunde ist in ihrer Dokumentation angegeben. Ein Beispiel hierfür ist der MAX1118EKA+T von Maxim Integrated. Die Abtastrate dieser Komponente beträgt 100 kHz. Das bedeutet, dass die analoge Spannung an ihrem Eingang 100.000 Mal pro Sekunde abgetastet wird. Aufgrund der enormen Anzahl an Abtastungen pro Sekunde kann die analoge Spannung mithilfe einer binären Interpretation exakt aufgezeichnet werden. Manchmal ist die Abtastrate eines ADC nicht hoch genug, um seinen Eingang exakt wiedergeben zu können. In diesem Fall kommt es zum sogenannten Aliasing. Die einzelnen Signale sind dann nicht mehr voneinander zu unterscheiden. Sie sind „Aliase“ voneinander. Nehmen Sie beispielsweise eine Videokamera, die mit 24 Frames pro Sekunde aufzeichnet. Das ist für die meisten Anwendungen ausreichend. Wenn Sie jedoch etwas betrachten möchten, das sich sehr schnell bewegt, kann es zu einer Verzerrung des Bildes kommen. Erinnern Sie sich zurück an den Effekt, der in den späten 90er-Jahren beim Betrachten der Aufnahme eines Fernsehers aufgetreten ist. Das im Fernseher zu sehende Bild flimmerte. Ursächlich hierfür war, dass die Bildwiederholungsrate des Fernsehers viel zu hoch war, als dass man das Fernsehbild mit den vorgegebenen Frames pro Sekunde hätte aufzeichnen können. Das Fernsehbild wäre verzerrt, da das Video tatsächlich nur eine Abfolge von Bildern ist. Zwischen den einzelnen Bildern geschieht viel mehr, als auf dem Video tatsächlich dargestellt wird. Dieser Effekt kann auch bei einem ADC auftreten. Um dies zu vermeiden, sollte die Abtastrate unbedingt mindestens doppelt so hoch sein wie die höchste Frequenz, die übertragen werden soll. Man spricht hierbei von der Nyquist-Rate.

Mit einer höheren Abtastrate arbeitet die Komponente genauer. Das ist jedoch nicht die einzige Möglichkeit, um die Genauigkeit zu steuern. Da in diesem Fall ein Analogsignal in einen Binärcode umgewandelt wird, ist die Anzahl der diskreten Stufen beschränkt, die zur Darstellung der Spannung zu einem bestimmten Zeitpunkt verwendet werden können. Die Anzahl der Bits, die zur Darstellung dieser Anzahl verwendet werden können, ist die Auflösung. Je höher die Auflösung des ADC ist, desto höher ist auch die Anzahl der diskreten Stufen. Um hier weiter ins Detail gehen zu können, muss man wissen, wie man die Anzahl der für einen ADC möglichen Stufen ermitteln kann. Ein ADC hat einen binären Ausgang, der repräsentativ für die Versorgungsspannung ist. Bei einer Versorgungsspannung von 10 V und einem 8-Bit-ADC sind 256 Stufen möglich Um die Auflösung zu ermitteln, verwenden Sie die Gleichung 2ⁿ. „2“ ist ein konstanter Wert und „N“ steht für die Bit-Anzahl. Somit erhalten wir für 2⁸ ingesamt 256 Stufen. Für 256 Stufen und eine Versorgungsspannung von 10 V erhalten wir für jede Stufe einen Wert von 39,0625 mV. Jede dieser Stufen hat einen eigenen Binärcode. Wenn man an einem ADC alle möglichen Eingangsoptionen von der niedrigsten bis hin zur höchsten durchläuft, erhält man eine treppenförmige Linie. Bei dieser Treppe handelt es sich um die Übertragungsfunktion des ADC. Abbildung 1 zeigt die Übertragungsfunktion für einen 3-Bit-ADC mit einer Referenzspannung von 2 V.

Abbildung 1: Übertragungsfunktion eines 3-Bit-ADC mit einer Referenzspannung von 2 V. (Mit freundlicher Genehmigung von Microchip Technology)

Für den 3-Bit-Wandler berechnet sich die Gesamtanzahl der Stufen mit der Formel 2ⁿ wie folgt:

Wie in Abbildung 1 ersichtlich, sind acht Stufen zwischen 000 und 111 vorhanden. Für jede Stufe erfolgt eine Erhöhung um ein LSB.

Wie zuvor erwähnt gibt es verschiedene Arten von ADC-Architekturen. Die drei verbreitetsten ADC-Architekturen sind SAR-, Delta-Sigma- (∆∑-) und Pipeline-Wandler. Alle diese Wandler wandeln ein analoges Eingangssignal in ein digitales Ausgangssignal um, wobei es bei der Art und Weise leichte Unterschiede gibt. Der SAR-Wandler tastet ein analoges Eingangssignal ab und hält es, wandelt es in ein digitales Signal um und gibt es dann weiter. Delta-Sigma-Wandler mitteln den Abtastwert über die zur Wandlung in ein digitales Signal benötigte Zeit. Bei Pipeline-Wandlern wird die Wandlung in verschiedene Stufen aufgeteilt, wodurch hohe Wandlungsgeschwindigkeiten möglich sind. Jede dieser Vorgehensweisen hat Vor- und Nachteile. Die SAR-Architektur ist benutzerfreundlich, hat üblicherweise einen geringen Stromverbrauch und bietet kurze Latenzzeiten mit hoher Genauigkeit. Sigma-Delta-Wandler bieten eine sehr hohe Auflösung sowie eine hohe Stabilität, sind energieeffizient und kostengünstig. Die Wandlungsgeschwindigkeit ist jedoch viel niedriger als bei SAR- und Pipeline-Architekturen. Der Pipeline-Wandler arbeitet im Vergleich zu den vorherigen Beispielen mit den höheren Geschwindigkeiten und höherer Bandweite. Die Auflösung ist dagegen geringer und der Stromverbrauch ist höher.

SAR-Wandler

SAR-Wandler (Wandler mit sukzessiver Approximation) sind die verbreitetste Art von ADCs. Sie verfügen häufig über eine I²C- oder SPI-Schnittstelle. Gelegentlich ist jedoch ein Parallelausgang vorhanden. Zur Verarbeitung des Analogsignals verfügen SAR-Wandler über eine Sample-and-Hold-Schaltung, um das Signal konstant zu halten. Ein Komparator vergleicht das analoge Eingangssignal mit einem internen DAC. Dieser DAC ist zu diesem Zeitpunkt auf die halbe Referenzspannung eingestellt. Ist die Eingangsspannung höher als die Vergleichsspannung des DAC, wird im MSB im „Successive-Approximation-Register“ der Wert „1“ gespeichert. Anschließend wird der DAC auf ¼ der Referenzspannung eingestellt und der Vorgang wird wiederholt. Die nächsten Werte für den DAC wären 1/8 und dann 1/16 der Referenzspannung usw., bis alle Bit in das Register geladen wurden. Diese Vorgehensweise lässt sich mit der Gewichtsbestimmung eines Gegenstands vergleichen, bei der man schrittweise Gewichte hinzufügt oder entfernt. Diese Analogie ist in Abbildung 2 dargestellt.

Abbildung 2: Illustrative Analogie zur Bestimmung eines digitalen Werts aus einem analogen Wert mit einem SAR-Wandler. (Mit freundlicher Genehmigung von Analog Devices)

Der große Block besteht aus insgesamt 45 Einheiten. Im ersten Versuch nimmt man 32 kleine Blöcke mit jeweils der Einheit „1“. Der Block ist schwerer als alle kleinen Blöcke zusammen. Die kleinen Blöcke bleiben daher liegen. Im nächsten Versuch werden 16 weitere kleine Blöcke hinzugefügt. Dadurch erhält man insgesamt 48 Blöcke (32 + 16), die zusammen schwerer sind als der große Block. Die 16 Blöcke werden daher wieder entfernt. Im nächsten Versuch werden dann acht weitere kleine Blöcke hinzugefügt und man erhält insgesamt 40 Blöcke. Diese acht Blöcke bleiben daher liegen. Im nächsten Schritt können vier weitere kleine Blöcke hinzugefügt werden. Mit den zwei kleinen Blöcken, die im nächsten Versuch hinzugefügt werden, erhält man insgesamt 46 Einheiten. Das ist wiederum zu schwer und die zwei Blöcke werden wieder entfernt. Im letzten Schritt wird nun ein kleiner Block hinzugefügt und das Gewicht der Blöcke ist auf beiden Seiten identisch. Jedes Mal, wenn Blöcke hinzugefügt wurden, wurde die Anzahl der Blöcke halbiert. Selbiges gilt auch für den Wert vom DAC im SAR-Wandler. Abbildung 3 zeigt das Blockdiagramm eines SAR-Wandlers.

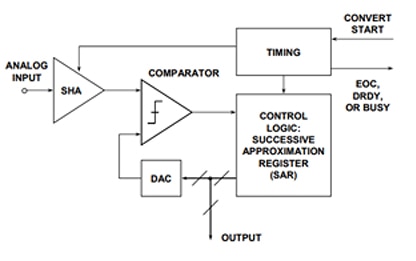
Abbildung 3: Funktionsblockdiagramm eines SAR-Wandlers. (Mit freundlicher Genehmigung von Analog Devices)

Ein Beispiel für einen SAR-Wandler ist der ADS7886SDBVT von Texas Instruments. Hierbei handelt es sich um einen 12-Bit-ADC-Wandler. Das bedeutet, dass zwischen 0 V und der Versorgungsspannung 4096 Stufen möglich sind. Die Abtastrate beträgt 1 MHz. Das Eingangssignal wird als eine Million Mal pro Sekunde abgetastet. Da die Leistung eines ADC vor dem Implementieren in ein fertiges Produkt getestet werden sollte, stellen die Hersteller häufig ein Evaluierungs-Tool für Tests zur Verfügung. Der ADS7886SDBVT bietet ein solches Evaluierungs-Tool, das ADS7886EVM. Mit diesem Tool lassen sich alle nötigen Tests sehr viel einfacher durchführen, da bereits eine Platine mit allen passiven Komponenten vorhanden ist, die erforderlich sind, um die Funktion des ADC zu testen.

Sigma-Delta-Wandler

Sigma-Delta-Wandler sind insbesondere dann eine überaus beliebte Wahl, wenn es auf hohe Auflösung und Präzision ankommt. Tonaufnahmen sind ein gutes Beispiel für den Einsatz von Sigma-Delta-Wandlern. Sigma-Delta-Wandler arbeiten mit einer Überabtastung der Eingangssignale. Die Nyquist-Rate ist bei Sigma-Delta-Wandlern nicht so entscheidend. Diese Wandler arbeiten optimal, wenn die Abtastrate etwa 20 Mal höher als die höchste abzutastende Frequenz ist. Das Ausgangssignal des Sigma-Delta-Wandlers wird in einen digitalen Dezimatorfilter eingespeist, der aus dem Bitstrom das finale Ausgangssignal macht. Zwischen dem digitalen Filter und dem Ausgang befindet sich häufig eine serielle Schnittstelle. Ein Beispiel für einen Sigma-Delta-Wandler ist der AD7175-2BRUZ von Analog Devices, Inc. Abbildung 4 zeigt das Funktionsblockdiagramm des AD7175-2BRUZ.

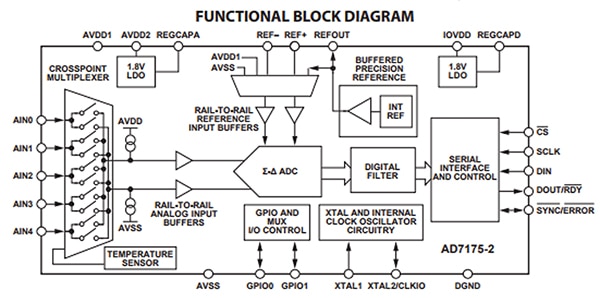
Abbildung 4: Funktionsblockdiagramm des Sigma-Delta-Wandlers AD7175-2BRUZ von Analog Devices. (Mit freundlicher Genehmigung von Analog Devices)

Dieser Sigma-Delta-Wandler bietet eine 24-Bit-Auflösung und eine Abtastrate von 250 kHz. Dadurch sind bis zu 16.777.216 Stufen möglich. Somit ist im Vergleich zum vorherigen Beispiel eine sehr viel höhere Auflösung möglich. Allerdings steht nur etwa ¼ der Abtastrate zur Verfügung. Wie im vorherigen Beispiel gibt es auch für den AD7175-2BRUZ eine Evaluierungskarte zu Testzwecken. Hierbei handelt es sich um die EVAL-AD7175-2SDZ, die eine einfache Möglichkeit zur Evaluierung des ADC darstellt.

Pipeline-Wandler

Der Pipeline-Wandler ist die schnellste Version. Ein Beispiel aus „ADC Architectures V: Pipelined Subranging ADCs“ bestätigt dies anhand eines 6-Bit-Pipeline-ADC. Die Sample-and-Hold-Schaltung funktioniert wie beim SAR-Wandler. Direkt im Anschluss folgt jedoch ein 3-Bit-Subranging-ADC mit Flash-Architektur, der das Signal digitalisiert. Die 3-Bit-Wandlung erfolgt für die drei höchstwertigen Bit. Anschließend erfolgt eine erneute Wandlung zurück in ein analoges Signal mit einem Subranging-DAC. Dieses Ausgangssignal wird vom Ausgangssignal der Sample-and-Hold-Schaltung subtrahiert, verstärkt und anschließend für die verbleibenden drei niederwertigsten Bit wieder in die zweite Stufe des 3-Bit-Subranging-ADC eingespeist. Diese Verfahrensweise wird im Blockdiagramm in Abbildung 5 dargestellt.

Abbildung 5: Funktionsblockdiagramm eines ADC mit Pipelined-(Subranging-)Architektur. (Mit freundlicher Genehmigung von Analog Devices)

Ein Beispiel für einen Pipeline-Wandler ist der ADC10080CIMT/NOPB von Texas Instruments. Hierbei handelt es sich um einen 10-Bit-ADC mit möglichen 1024 Stufen und einer Abtastrate von bis zu 80 Megasamples pro Sekunde. Anwendungsbeispiele für diese Komponente sind Ultraschall- und Abbildungssysteme, Instrumentensysteme, Datenerfassungssysteme oder jegliche Anwendungen, die eine schnelle Wandlung von Signalen erfordern. Betrachtet man das Blockdiagramm des ADC10080CIMT/NOPB, kann man erkennen, wie der Wandler gemäß obiger Beschreibung aufgebaut ist. Abbildung 6 zeigt das Blockdiagramm aus dem Datenblatt zum ADC1008CIMT/NOPB.

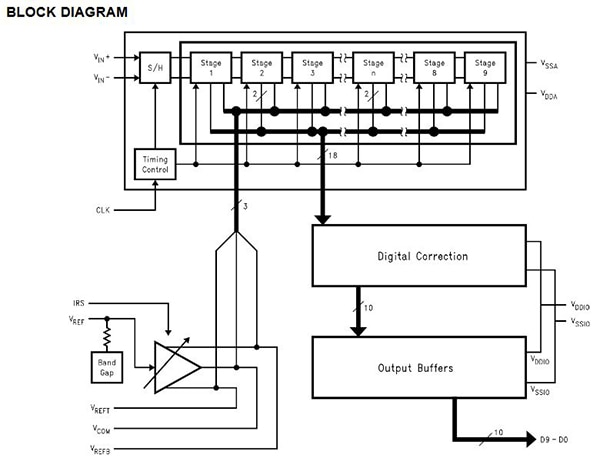
Abbildung 6: Funktionsblockdiagramm des ADC10080CIMT/NOPB von Texas Instruments. (Mit freundlicher Genehmigung von Texas Instruments)

DAC mit binär gewichteten Stromquellen

Bis jetzt wurde in diesem Artikel ausschließlich die Datenkonvertierung durch ADCs behandelt. Häufig ist es jedoch erforderlich, binäre Daten wieder in ein analoges Signal umzuwandeln. Hier kommt der sogenannte Digital-Analog-Wandler ins Spiel. In der Schule wird als Erstes häufig der DAC mit binär gewichteten Stromquellen behandelt. In diesem Wandlertyp wird ein aus mehreren Widerständen bestehendes System verwendet, deren Ausgänge alle an demselben Summenwiderstand zusammenlaufen. Die höherwertigen Bit liefern einen höheren Strom als die niederwertigen Bit. Hierfür wird ein umgekehrt proportionales Widerstandsnetzwerk aufgebaut. Da jedes binäre Bit des digitalen Codes denselben Spannungswert hat, ermöglichen die höherwertigen Bit bei Anwendung von umgekehrt proportionalen Widerständen auf jedes einzelne Bit einen höheren Stromfluss. Diese Konvertierungsmethode ist nicht mehr sehr weit verbreitet, da es heutzutage einfachere Methoden gibt. Sie eignet sich jedoch sehr gut, um die grundlegende Funktionsweise von DACs zu beschreiben. Die größte Schwierigkeit bei dieser Methode besteht darin, Widerstände mit verschiedenen Werten zu finden, die zusammen verwendet werden können. Der Toleranzbereich müsste unglaublich eng sein und es bereitet einfach sehr viel weniger Probleme, Widerstände mit ähnlichen Werten zu finden, als Widerstände mit mehreren verschiedenen Werten, wie Sie bei dieser Methode benötigt werden. Abbildung 7 zeigt diese Architektur anhand des Schaltplans eines Netzwerks aus binär gewichteten Widerständen.

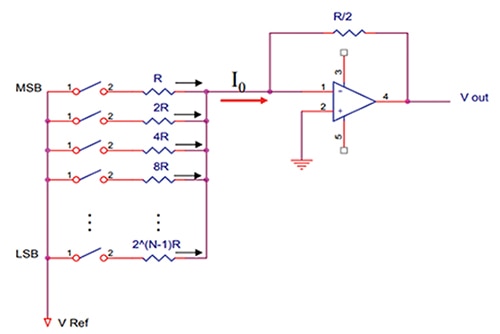
Abbildung 7: Schaltplan eines Netzwerks aus binär gewichteten Widerständen. (Mit freundlicher Genehmigung des Georgia Institute of Technology)

String-DAC

Eine weitere beliebte Architektur für DACs ist der sogenannte String-DAC. Hierbei handelt es sich um die einfachste, aber auch die am wenigsten lineare Architektur, die gelegentlich auch als Kelvin-Spannungsteiler bezeichnet wird. Bei dieser Architektur werden mehrere Widerstände gleicher Größe in Reihe geschaltet. Dieses Widerstandsnetzwerk ist an der Oberseite an eine Referenzspannung angeschlossen, vor den Widerständen befindet sich ein Widerstand mit hoher Impedanz und jeder Knoten verfügt über einen Schalter, der einem Binärcode zugeordnet ist. Diese Schalter werden geschlossen, wenn der entsprechende Binärcode von der Komponente gelesen wird. Auf diese Weise kann ein analoger Spannungswert verwendet werden, der vom binären Eingangssignal abhängt. Abbildung 8 stammt aus einem Video mit dem Titel „What is a String DAC?“ von Texas Instruments. Der Code 010 steht für den Dezimalwert 2. Der Schalter bei 010 ist gerade geschlossen, sodass die Gleichspannung an diesem Knoten an den Summierverstärker weitergegeben werden kann.

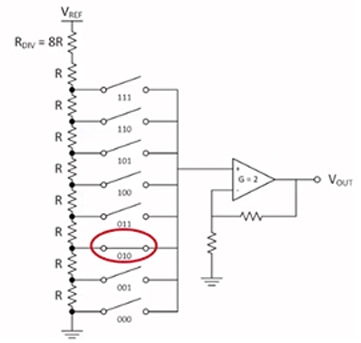
Abbildung 8: Schaltplan eines String-DAC. (Mit freundlicher Genehmigung von Texas Instruments)

String-DACs lassen sich einfach herstellen, da ausschließlich Widerstände gleicher Größe verwendet werden (den Widerstand mit hoher Impedanz ausgenommen). Ein Beispiel für einen String-DAC ist der AD5683RBRMZ von Analog Devices Inc. Hierbei handelt es sich um einen 16-Bit-String-DAC mit SPI-Schnittstelle. Abbildung 9 zeigt ein Funktionsblockdiagramm dieser Komponente und Abbildung 10 zeigt den ohmschen Spannungsteiler. Auch für dieses Produkt gibt es mit dem EVAL-AD5683RSDZ ein Evaluierungs-Tool.

Abbildungen 9 und 10: Funktionsblockdiagramm des AD5683RBRMZ von Analog Devices (links) und seines Netzwerks aus ohmschen Spannungsteilern (rechts). (Mit freundlicher Genehmigung von Analog Devices)

R-2R

Das R-2R-Netzwerk ist eine weitverbreitete DAC-Architektur. Bei dieser Architektur kommen nur Widerstände in zwei Größen zum Einsatz. Dabei spielt ihre Größe keine Rolle, solange 2R doppelt so groß wie R ist. Dadurch sind R-2R-DACs sehr gut skalierbar. Unabhängig von der Bit-Anzahl des DAC werden immer nur Widerstände in zwei Größen benötigt. Abbildung 11 zeigt ein 4-Bit-R-2R-Kettennetzwerk.

Abbildung 11: Schaltplan eines R-2R-DAC. (Mit freundlicher Genehmigung von Analog Devices)

Dieses Spannungsteilernetzwerk funktioniert nach dem Thévenin-Theorem, um schlussendlich das Thévenin-Äquivalent (die Ersatzspannungsquelle) für das gesamte „R“-Netzwerk zu erhalten. Für jede Stufe ist das Doppelte der Spannung der letzten Stufe zulässig. In diesem Beispiel gilt Folgendes: Wäre Vref gleich 5 V, dann könnte die am weitesten links liegende Stufe für das LSB nur eine Spannung von 0,3125 V erzeugen. Von links nach rechts gilt für die proportionale Ausgangsspannung Folgendes:

Dies gilt für alle digitalen Eingangswerte. X0 ist das LSB und X3 ist das MSB. Für eine Referenzspannung von 5 V erhalten wir Folgendes:

Um mit derselben Logik den Wert der Analogspannung für das MSB zu bestimmen, könnte man so vorgehen:

Für einen binären Eingangswert von 1111 wäre die Ausgangsspannung nicht gleich 5 V. Erinnern Sie sich an die Ausführungen zur Auflösung. Mit einem 4-Bit-DAC sind 16 Stufen möglich. Gemäß der Rechnung 2⁴ ergeben sich 16 Stufen. Das LSB liegt bei 0,3125 V. Würde man 0,3125 mit 16 multiplizieren, würde man als Ergebnis den Wert 5 erhalten. Das ist jedoch irreführend, da für eine der Stufen eine Erdungsspannung von 0 V verwendet wird, um den binären Wert 0000 darzustellen. Somit ist die höchste erreichbare Spannung die Versorgungsspannung minus eine LSB-Spannung. Somit erhalten wir für die Spannung den Wert 4,6875 V.

Ein Beispiel für einen R-2R-DAC ist der DAC8734SPFB von Texas Instruments. Hierbei handelt es sich um einen 16-Bit-Wandler, der die Skalierbarkeit dieser Komponenten demonstriert. Das Layout für das R-2R-Netzwerk ist dem oben beschriebenen sehr ähnlich. Abbildung 12 zeigt das R-2R-Netzwerk für den DAC8734SPFB. Für den DAC8734SPFB gibt es mit dem DAC8734EVM ebenfalls ein Evaluierungs-Tool.

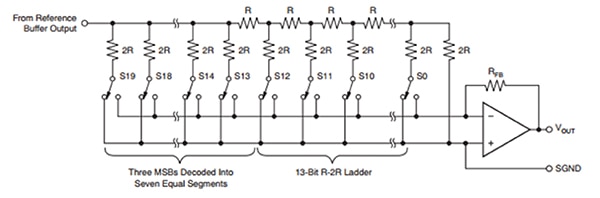
Abbildung 12: Schaltplan des R-2R-DAC DAC8734SPFB von Texas Instruments. (Mit freundlicher Genehmigung von Texas Instruments)

Neben den in diesem Artikel behandelten gibt es noch viele weitere ADC-/DAC-Architekturen. Hier soll jedoch nur auf die am weitesten verbreiteten Architekturen eingegangen werden. Diese Komponenten sind für die digitale Signalverarbeitung unerlässlich. Ohne ADCs/DACs wäre es nicht möglich, analoge Ausgangswerte in der digitalen Signalverarbeitung zu nutzen und umgekehrt. Für den Laien mag das eine Selbstverständlichkeit sein, doch für Ingenieure, die analoge Komponenten mit digitalen Systemen verbinden müssen, ist dies einer der wichtigsten Schritte, den es zu bedenken gilt. Denken Sie bei der Analog-Digital-Wandlung zurück an die Analogie mit den zwei Personen, die verschiedene Sprachen sprechen. Ohne Übersetzer könnten diese Personen nicht miteinander kommunizieren. Ebenso müsste man ohne ADC-/DAC-Komponenten für eine Anwendung entweder rein analoge oder rein digitale Komponenten verwenden. ADC-/DAC-Komponenten stellen praktisch die Verbindung zwischen diesen zwei Welten her.

Ressourcen

1. „AVR127: Understanding ADC Parameters“. Mai. 2016.
2. „Choose the right A/D converter for your application“. Abgerufen am 8. Mai. 2017.
3. Kester, Walt. „ADC Architectures II: Successive Approximation ADCs“. Okt. 2008.
4. Kester, Walt. „ADC Architectures III: Sigma-Delta ADC Basics“. Okt. 2008.
5. Kester, Walt. „ADC Architectures IV: Sigma-Delta ADC Advanced Concepts and Applications“. Okt. 2008.
6. Kester, Walt. „ADC Architectures V: Pipelined Subranging ADCs“. Okt. 2008.
7. Kester, Walt. „DAC Interface Fundamentals“. Okt. 2008.
8. Kester, Walt. „Basic DAC Architectures II: Binary DACs“. Okt. 2008.
9. Lee, J., Jeelani K., Beckwith, J. „Digital to Analog Converter“. Abgerufen am 8. Mai. 2017
10. Poole, Matt. „What is a String DAC?“. 4. April 2016