Schnelle und einfache Messungen des Frequenzgangs mit einem Oszilloskop

Müssen Sie den Frequenzgang eines Filters überprüfen oder die Bandbreite eines Verstärkers messen? Es ist nicht nötig, einen Frequenzgang- oder Netzwerkanalysator zu bemühen. Sie können diese Messung mit Hilfe eines Oszilloskops und eines Rechtecksignals mit schneller Flanke durchführen.

Frequenzgangmessungen erfordern einen Eingang mit konstanter Amplitude über den gesamten Frequenzbereich der Messung. Die drei Arten von Signalen mit einem flachen Frequenzspektrum sind Sinus, Impuls und breitbandiges Rauschen. Von den drei Möglichkeiten liefert die Impulsantwort das schnellste Ergebnis. Die nächste Frage lautet also: Wie erhält man eine Impulswellenform?

Erinnern Sie sich an das Einmaleins der Schaltungsanalyse: Der Impuls ist die Ableitung der Sprungfunktion (auch Schrittfunktion oder Stufenfunktion genannt). Wenn Sie die Sprungantwort des zu prüfenden Geräts haben, können Sie sie durch Differenzieren in die Impulsantwort umwandeln. Die meisten Tischoszilloskope enthalten Integration und Differenzierung als Teil ihrer mathematischen Funktionspakete. In diesem Beispiel wird das 500MHz-Oszilloskop HDO 4054A von Teledyne LeCroy verwendet. Die Bandbreite des Oszilloskops muss die des zu messenden Geräts um den Faktor fünf übersteigen, um systematische Amplitudenfehler unter einem halben Dezibel (dB) zu halten. Ein alternatives Oszilloskop ist das WAVESURFER-3054Z von Teledyne LeCroy.

Wie erhält man eine Sprungfunktion? Das ist einfach: Die isolierte ansteigende oder abfallende Flanke einer Rechteckwelle oder eines Impulses ist eine Sprungfunktion: Die Differenzierung der Sprungfunktion ergibt einen Impuls. Dies ist in Abbildung 1 für die ansteigende Flanke einer 10kHz-Rechteckwelle dargestellt (oberer Signalverlauf).

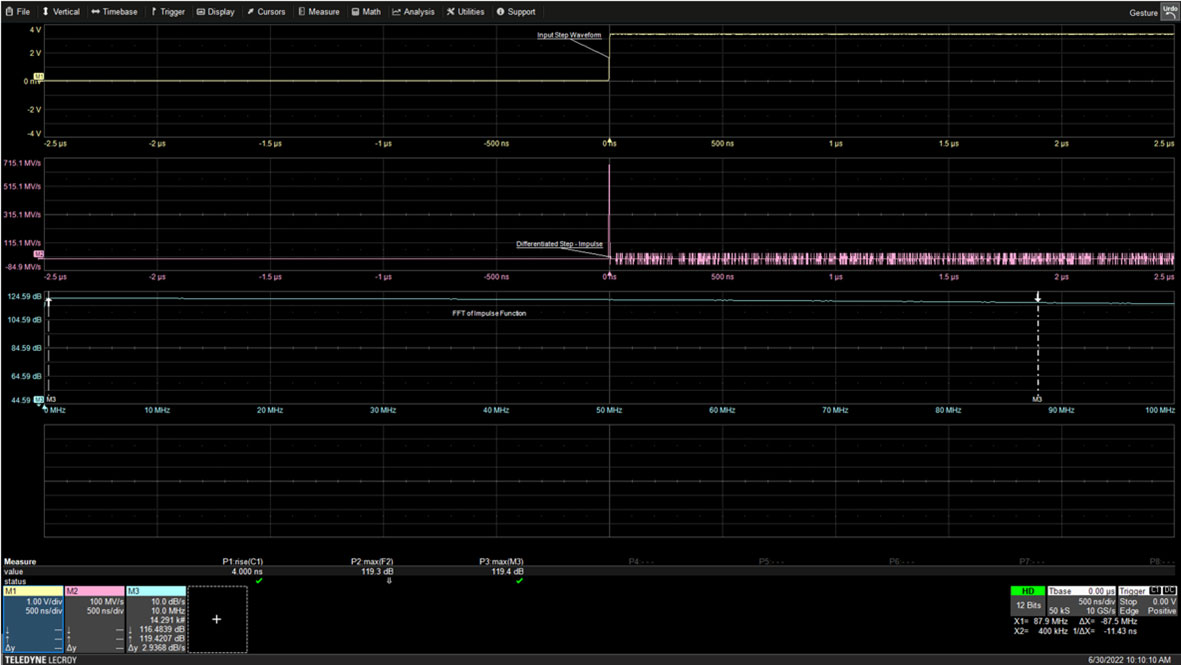Abbildung 1: Die ansteigende Flanke einer 10kHz-Rechteckwelle wird durch Differenzierung zu einer Impulsfunktion. Das Spektrum des Impulses ist flach mit einer Bandbreite, die umgekehrt proportional zur Anstiegszeit der Rechteckwelle ist. (Bildquelle: Art Pini)

Das Oszilloskop erfasst nur 5 Mikrosekunden (ms) über die Flanke. Der Rest der 100 ms langen Rechteckwelle ist nicht auf dem Bildschirm zu sehen. Die Sprungfunktion wird mithilfe der mathematischen Fähigkeiten des Oszilloskops differenziert und als mittlere Kurve angezeigt. Die schnelle Fourier-Transformation (FFT) des Impulses ist im unteren Signalverlauf dargestellt. Die Bandbreite des Impulses wird durch die Anstiegszeit der Rechteckwelle bestimmt. In diesem Fall wird die Anstiegszeit mit 4 Nanosekunden (ns) gemessen, wie im Messparameter P1 unter den Leiterbahnrastern angegeben. Die Bandbreite des Impulses kann als 0,35 geteilt durch die Anstiegszeit für ein Oszilloskop mit einpoligem Amplitudengang berechnet werden.

Das Ergebnis ist in diesem Fall 87,5 MHz, was durch den rechten Cursor auf der FFT-Anzeige mit einem numerischen Wert im Anmerkungsfeld der mathematischen Signalverlaufs M3 gekennzeichnet ist. Die Amplitude der FFT bei 87,5 MHz beträgt 116,48 dB im Vergleich zur maximalen FFT-Amplitude von 119,43 dB oder etwa -3 dB vom Maximum, was die Signalbandbreite bestätigt.

Die Signalquelle für die Frequenzgangmessung sollte Rechteckwellen oder Impulswellenformen bieten, die schnell genug sind, um eine ausreichende Messbandbreite zu gewährleisten. Die in der Abbildung verwendete 4ns-Flanke wurde von einem 150MHz-Arbiträrsignalgenerator T3AWG2152-D von Teledyne LeCroy erzeugt. Eine Signalquelle mit einer noch kürzeren Anstiegszeit von 2 ns ist der T3AFG200 von Teledyne LeCroy, ein 200MHz-Arbiträrfunktionsgenerator für 2,4 Giga-Samples pro Sekunde (GS/s). Die Anstiegszeit von 2 ns bietet eine Signalbandbreite von 175 MHz.

Frequenzgang eines digitalen Tiefpassfilters

Im folgenden Beispiel wird der Frequenzgang eines digitalen Tiefpassfilters mit dem Oszilloskop HDO4054A von Teledyne LeCroy und dem T3AWG2152-D gemessen (Abbildung 2). Diese Filtermessungen erscheinen in der linken Spalte der Kurven.

Das Sprungsignal wird an den Filtereingang angelegt. Der Filterausgang wird differenziert und angezeigt. Beachten Sie, dass der Filter die Impulsantwort aufgrund seiner begrenzten Bandbreite verbreitert hat. Der Filterausgang wird auf die FFT angewendet und gemittelt, um den Betragsfrequenzgang des Filters zu erhalten.

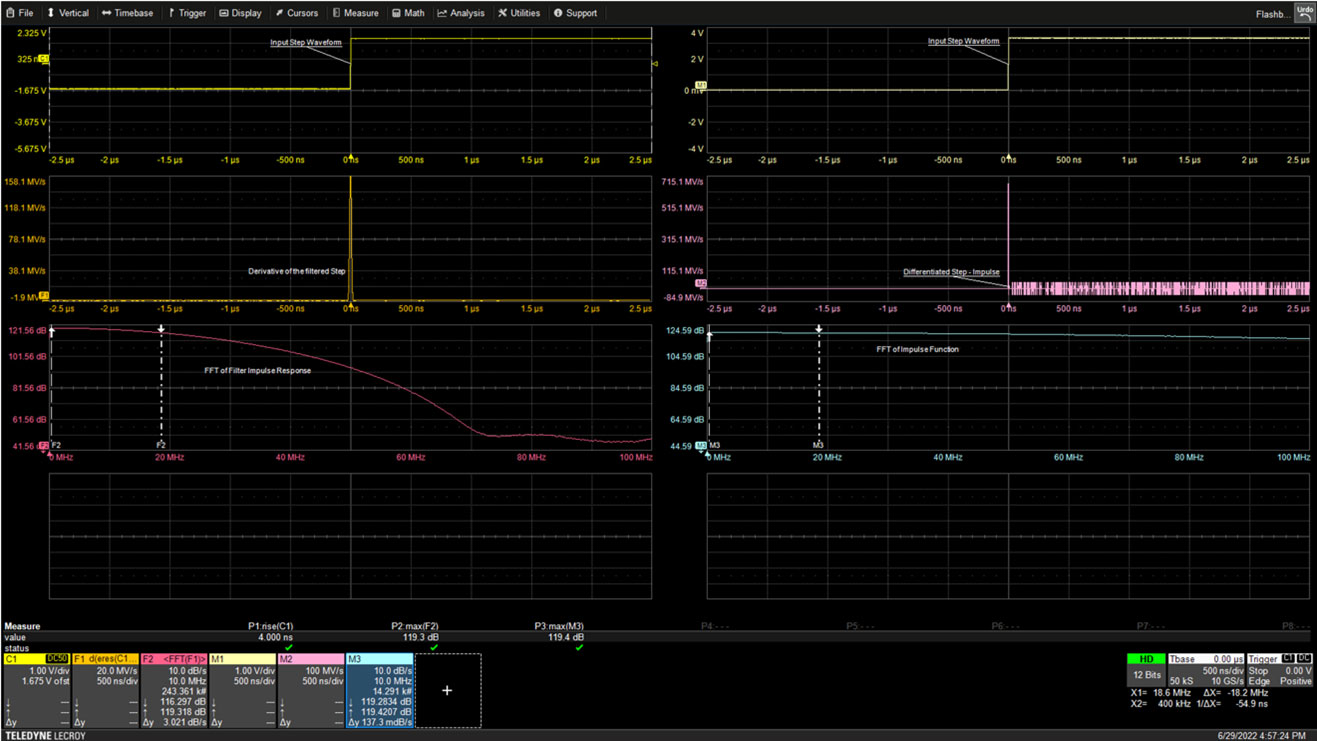Abbildung 2: Das Sprungsignal, die Kurve oben links, wird an den Filtereingang angelegt. Der Filterausgang wird differenziert und in der mittleren linken Kurve angezeigt. Die FFT des gefilterten Signals, unten links, zeigt den Frequenzgang des Filters. (Bildquelle: Art Pini)

Die Cursor auf der FFT des Filterausgangs zeigen die -3dB-Bandbreite im Anmerkungsfeld F2 bei einer Frequenz von 18,6 MHz an: Dies ist die Filterbandbreite. Gleichzeitig zeigt der Cursor auf der FFT der Impulsfunktion in der unteren rechten Kurve eine Dämpfung von nur 0,12 dB im M3-Anmerkungsfeld bei 18,6 MHz an, was darauf hindeutet, dass die Signalquelle im Wesentlichen flach ist.

Fazit

Wie gezeigt, kann die Reaktion frequenzabhängiger Komponenten schnell und einfach gemessen werden, ohne auf Netzwerk- oder Frequenzganganalysatoren zurückgreifen zu müssen. Es braucht nur grundlegende Oszilloskopfunktionen, die auf ein Rechtecksignal mit schneller Flanke angewendet werden.