Wie man die Macht des Bode-Diagramms nutzt, um die Stabilität eines Stromkreises zu gewährleisten

In den 1930er Jahren entwickelte Hendrik Wade Bode einen intuitiven Verstärkungs-/Phasenansatz, bei dem die Stabilität einer Schaltung das einzige Ziel war. Daraus entstand der so genannte Bode-Plot, eine intuitive grafische Darstellung der Verstärkung, der Phase und des Rückkopplungssystems einer Schaltung oder eines Verstärkers über der Frequenz.

In Anbetracht der Nützlichkeit und Wichtigkeit dieses Verfahrens wollen wir uns die Zeit nehmen, die Bode-Stabilitätsanalyse anzuwenden, um den Betrag des Rückkopplungsfaktors in Dezibel (dB) und den Phasengang (in Grad) eines Verstärker und Kreises mit offener Regelschleife zu untersuchen. Dieser Blog befasst sich mit den Konzepten und beschreibt, wie man einen „brummenden“ Schaltkreis vermeiden kann, wenn das Hauptziel die Frequenzstabilität ist.

Um diese Technik zu üben, können Sie eine druckbare Version eines Bode-Diagramms aus den Ressourcen im Online-Handbuch für Innovationen von DigiKey herunterladen.

Einpoliges Bode-Diagramm

Die Konfiguration der einpoligen Schaltung ermöglicht es, dass V_IN-Gleichspannungssignale direkt an V_OUT weitergeleitet werden, während V_OUT bei höheren Eingangsfrequenzen gleich Null Dezibel (dB) ist. Die Konstruktion des Bode-Plots ist einfach. Die Einheiten auf der x-Achse sind logarithmische Frequenzen, und die lineare y-Achse ist entweder die Verstärkung in Dezibel oder die Phase in Grad. Es gibt eine ganze Reihe von Formeln, die Sie bei der Erstellung eines Bode-Diagramms anwenden können, aber lassen Sie uns kurz auf die schnelle Lösung eingehen.

Die Einfachheit des Bode-Plots besteht darin, dass zum Zeichnen der Graphen nur ein Lineal und die Kenntnis einiger weniger Regeln erforderlich sind (Abbildung 1).

Abbildung 1: Ein einpoliges Bode-Diagramm zur Veranschaulichung von Amplituden- und Phasenverschiebung verwendet gerade Linien zur Darstellung des Frequenz- und Phasengangs der Schaltung. (Bildquelle: Bonnie Baker)

Die beiden Diagramme in Abbildung 1 zeigen die Frequenz in Abhängigkeit von der Verstärkung und der Phase für ein einpoliges Widerstands-/Kondensatorpaar. Die Frequenzbereiche der x-Achse des oberen und unteren Diagramms liegen zwischen 1 Hertz (Hz) und 10 Megahertz (MHz). Der y-Achsenbereich der oberen Grafik reicht von 0 Dezibel (dB) bis 100 dB, wobei der 1-Hz-Signalwert 100 dB entspricht. Dieser Wert steht im Einklang mit einem Verstärkungsfaktor von 100.000 x V_IN. Die blaue Kurve ist die Verstärkungsantwort mit einem Einzelpol bei f_P oder 100 Hz, wobei R gleich 159 Kiloohm (kΩ) und C gleich 10 Nanofarad (nF) ist.

Wenn die Frequenz über die Polfrequenz (f_P) hinaus ansteigt, fällt die blaue Kurve mit einer Rate von -20 dB/Dekade oder -6 dB/Oktave. Diese Dämpfungsrate ist die erste Bode-Plot-Faustregel, die man sich merken sollte: Jeder Pol im Schaltkreis fällt mit einer Rate von -20 dB/Dekade, beginnend bei der Polfrequenz. Wenn also zwei Pole V_OUT im gleichen Frequenzbereich abschwächen, beträgt die Abschwächungsrate -40 dB/Dekade.

Das untere Diagramm in Abbildung 1 zeigt die Phase dieser einpoligen Schaltung. Bei 1 Hz ist die Phase des R/C-Netzes 0 Grad (°). Eine Dekade vor f_P, d. h. in diesem Fall 10 Hz, beginnt die einpolige Phase mit -45°/Dekade auf ihr Ziel von -90° abzufallen.

Für den Phasengang des Pols gelten mehrere Regeln. Die zweite Bode-Plot-Faustregel für die Polschaltung lautet, dass die Phase bei f_P gleich -45° ist. Die dritte und vierte Bode-Plot-Regel beschreiben den Phasenpunkt der Abschwächung und des Abschlusses. Die einpolige Phase beginnt eine Dekade vor der Polfrequenz (f_P) zu fallen und pendelt sich schließlich eine Dekade nach f_P bei -90° ein.

Bode-Diagramm mit einer Nullstelle

Das Bode-Diagramm mit einer Nullstelle spiegelt die umgekehrten Regeln des Bode-Diagramm mit einem Pol wider. Die Positionen wechseln mit den gleichen Werten für R und C, um V_IN-Gleichspannungen zu verhindern, während die höhere Frequenz durch den Kondensator fließen kann (Abbildung 2).

Abbildung 2: Bode-Diagramm mit einer Nullstelle zur Darstellung von Betrags- und Phasenverschiebung. (Bildquelle: Bonnie Baker)

Wenn die Frequenz über f_Z hinaus ansteigt, steigt die blaue Kurve um +20 dB/Dekade an. Das untere Diagramm in Abbildung 2 zeigt die Phase dieser Schaltung mit einer Nullstelle. Eine Dekade vor f_Z beginnt die Phase mit einzelner Nullstelle mit einer Rate von +45°/Dekade in Richtung ihres Ziels von +90° anzusteigen. Die Phase des Nullstellenstromkreises ist bei f_Z gleich +45°.

Die Werte in Abbildung 1 lassen sich wie folgt zusammenfassen: Die Polstelle ist f_P, und die Verstärkung nach f_P hat eine Steigung von -20 dB/Dekade. Die Phase hat eine Neigung von -45°/Dekade über f_P, und die Phase beginnt ihre Dämpfung bei 0,1 x f_P und pendelt sich bei 10 x f_P auf -90° ein. Die Werte in Abbildung 2 lassen sich wie folgt zusammenfassen: Der Nullpunkt liegt bei f_Z, und die Verstärkung nach f_Z hat eine Steigung von +20 dB/Dekade. Die Phase hat eine Neigung von +45°/Dekade über f_Z, und die Phase beginnt ihre Dämpfung bei 0,1 x f_Z und pendelt sich bei 10 x f_Z auf +90° ein.

Bode-Diagramm eines Verstärkers mit offener Regelschleife

Der Frequenzbetrieb eines Standard-Operationsverstärkers kann mehrere Pole und Nullstellen in der Übertragungsfunktion von Sub-Hertz bis zur Null-DB-Grenzfrequenz aufweisen. Die Bode-Darstellung des Verstärkers ist kein Hexenwerk, es müssen nur die Regeln beachtet werden (Abbildung 3).

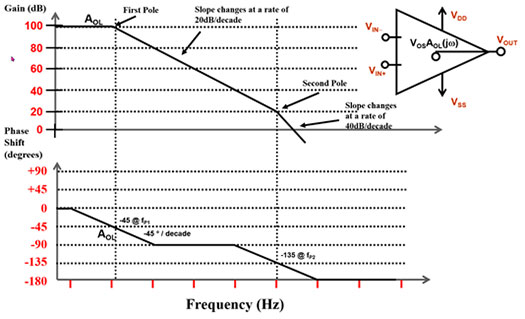Abbildung 3: Mögliches Bode-Diagramm eines Operationsverstärkers zur Veranschaulichung von Betrags- und Phasenverschiebung. (Bildquelle: Bonnie Baker)

Abbildung 3 zeigt das Beispiel eines Operationsverstärkers mit zwei Polen (f₁ und f₂) in der Übertragungsfunktion. Mit den beiden Polen sinkt die Verstärkung um jeweils -20 dB/Dekade, und die Phase fällt auf insgesamt -180 Grad.

Wir haben bereits einen guten Anfang gemacht bezüglich der Konstruktion von Bode-Diagrammen, aber gehen wir weiter in Richtung der realen Welt, wo es ein Rückkopplungssystem in der Mischung gibt.

Stabilität des Verstärkersystems im geschlossenen Regelkreis

Sie werden immer ein Rückkopplungsnetzwerk finden, wenn Sie sich etwas Zeit bei der Betrachtung von Schaltungen mit Operationsverstärkern nehmen. Das klassische Operationsverstärker-Rückkopplungsnetzwerk hat ein Vorwärtsverstärkungselement (A_OL(jω)) und ein Rückkopplungselement (β(jω)).

Abbildung 4: Klassisches Operationsverstärker-Rückkopplungsnetzwerk mit einem Vorwärtskopplungselement (AOL(jω)) und einem Rückkopplungselement (β(jω)). (Bildquelle: Bonnie Baker)

In Abbildung 4 ist die Verstärkung der offenen Schleife des Operationsverstärkers (A_OL) vergleichsweise groß, und der Rückkopplungsfaktor ist relativ klein. Bei dieser Konfiguration wird der Ausgang an den invertierenden Anschluss zurückgeführt, wodurch eine negative Rückkopplung entsteht, die den Ausgang unter Kontrolle bringt. Wir werden den Kehrwert von β oder 1/β verwenden, um die Stabilität einer Operationsverstärkerschaltung zu bestimmen.

Am einfachsten lässt sich 1/β berechnen, indem man eine Quelle, V_STABILITY genannt, an den nicht-invertierenden Eingang des Operationsverstärkers legt. Mit dieser Berechnungsstrategie lässt sich die Stabilität der Schaltung hervorragend ermitteln (Abbildung 5).

Abbildung 5: Eine nicht-invertierende Operationsverstärkerschaltung a.) und eine invertierende Operationsverstärkerschaltung b.) haben beide eine fiktive V_STABILITY-Spannungsquelle an ihrem nicht-invertierenden Eingang, um eine genaue Berechnung des 1/β-Faktors bzw. der Rauschverstärkung der Schaltung zu ermöglichen. (Bildquelle: Bonnie Baker)

Bei der Betrachtung der Schaltungen in Abbildung 5 fällt auf, dass die Rückkopplungsschaltungen von der nicht-invertierenden Klemme zum Ausgang identisch sind. Die Lage der V_STABILITY-Spannungsquelle ermöglicht eine genaue Berechnung des 1/β-Faktors bzw. der Rauschverstärkung der Schaltung.

Die 1/β-Stabilitätsanalyse verwendet V_STABILTIY. Wenn man davon ausgeht, dass die Verstärkung der offenen Regelschleife des Operationsverstärkers unendlich ist, ist die Übertragungsfunktion der beiden Schaltungen gleich:

Gleichung 1

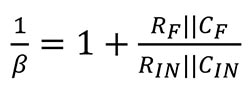Gleichung 2

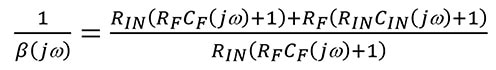Gleichung 3

Wenn die Frequenzkomponenten aus Gleichung 3, jω, gleich Null sind:

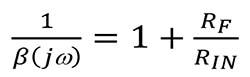Gleichung 4

Wenn jω in Gleichung 3 gegen Unendlich geht:

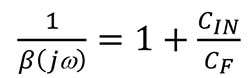Gleichung 5

Die Frequenzen für den Nullpunkt (f_Z) und den Pol (f_P) von 1/β sind:

Gleichung 6

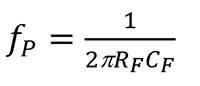Gleichung 7

Die Bode-Plots der 1/β-Stabilitätsanalysekurven, die den oben genannten Regeln entsprechen, sind in Abbildung 6 dargestellt.

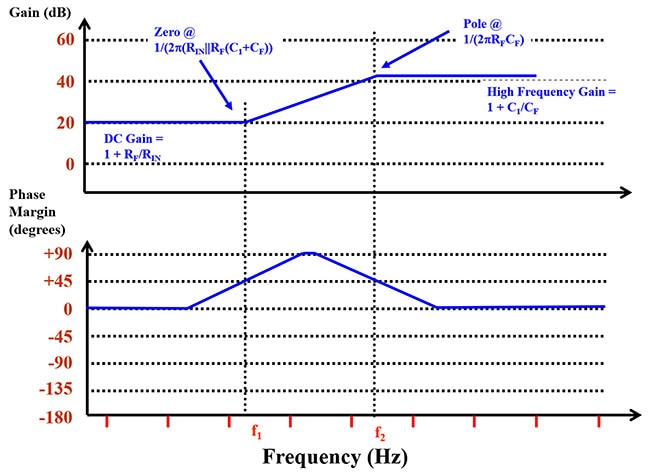Abbildung 6: Der 1/β-Frequenzgang für Abbildung 5 a.) und b.) ist identisch. Der Nullpunkt tritt bei einer niedrigeren Frequenz auf, der Pol bei einer höheren Frequenz. (Bildquelle: Bonnie Baker)

Abbildung 6 beschreibt den Frequenz- und Phasengang der 1/β-Rauschverstärkung der Operationsverstärkerschaltung. Diese Abbildung fasst die Gleichungen 4 bis 7 in grafischer Form zusammen. Die Gleichungen 4 und 5 definieren die DC-Verstärkung und die ¥-Verstärkung. Die Gleichungen 6 und 7 bestimmen den Nullpunkt und den Pol der Schaltung. Die Informationen in den Abbildungen 3 und 6 sind der erste Schritt zur Ermittlung der Stabilität einer Operationsverstärkerschaltung, indem die Übertragungsfunktion des Systems und die Lage der Pole und Nullstellen definiert werden. Der letzte Schritt besteht darin, die Abbildungen 3 und 6 in einem Diagramm zu überlagern.

Bestimmung der Systemstabilität

Der Schnittpunkt bzw. die Schließgeschwindigkeit von offenem und geschlossenem Regelkreis bestimmt die Phasenverschiebung der Schaltung. Im Allgemeinen deutet eine Schließrate von 30 dB oder weniger auf einen stabilen Stromkreis hin. Eine Schließrate von größer als 30 dB deutet auf einen instabilen Schaltkreiszustand hin (Abbildung 7).

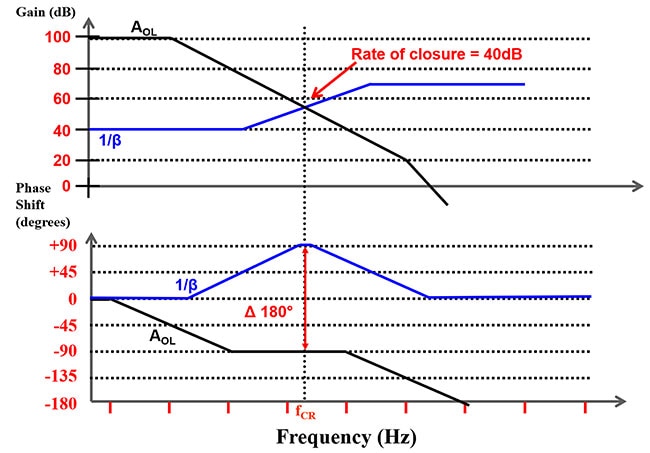Abbildung 7: Überlagerung des AOL-Verstärkungs- und Phasengangs des Operationsverstärkers mit dem 1/β-Verstärkungs- und Phasengang. (Bildquelle: Bonnie Baker)

In Abbildung 7 ist die Schließungsrate zwischen der A_OL- und der 1/β-Verstärkungskurve gleich 40 dB. Eine Schließrate von 40 dB weist auf eine Phasenverschiebung von mehr als 135° hin, was auf einen instabilen Schaltkreis hinweist. Bei dieser Konfiguration führt die Schließgeschwindigkeit von 180° zu einem schwingenden Kreislauf.

Es gibt viele Lösungen für das oben genannte Problem. Die ohmschen oder kapazitiven Werte können durch Verschieben der Pol- und Nullfrequenzen variiert werden. Eine andere Alternative ist die Auswahl eines anderen Operationsverstärkers (Abbildung 8).

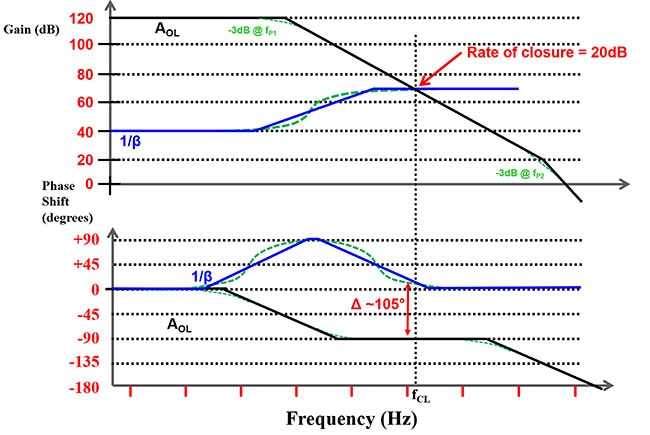Abbildung 8: Verwendung eines Operationsverstärkers, dessen Bandbreite höher ist als die des Operationsverstärkers in Abbildung 7, ohne dass sich die Null- und Polfrequenzen ändern. (Bildquelle: Bonnie Baker)

In Abbildung 8 ist die Bandbreite des Operationsverstärkers etwa zwei Dekaden höher, ohne dass eine Änderung des 1/β-Netzwerks vorgenommen wurde. Die grün gestrichelten Linien spiegeln die tatsächlichen Berechnungen wider und ergeben ein realistischeres Bode-Diagramm. Durch die Erhöhung der Verstärkerbandbreite ändert sich die Schließungsrate von 40 dB auf 20 dB. Die resultierende Phasenverschiebung beträgt nun ~105°, was auf eine stabile Schaltung hinweist.

Die grün gepunkteten Linien in Abbildung 8 gehen über die Erstellung des Bode-Diagramms mit Lineal und Bleistift hinaus, indem sie die reale Reaktion einbeziehen.

Messkreisverstärkung und Phase

Für die Messung der Verstärkung und der Phase eines Verstärkerschaltkreises ist ein Funktionsgenerator erforderlich, der das Eingangssignal liefert, sowie ein Netzwerkanalysator (Abbildung 9). Abgebildet ist der analoge 3-GHz-HF-Sweep-Funktionsgenerator LS3081B von Tabor Electronics.

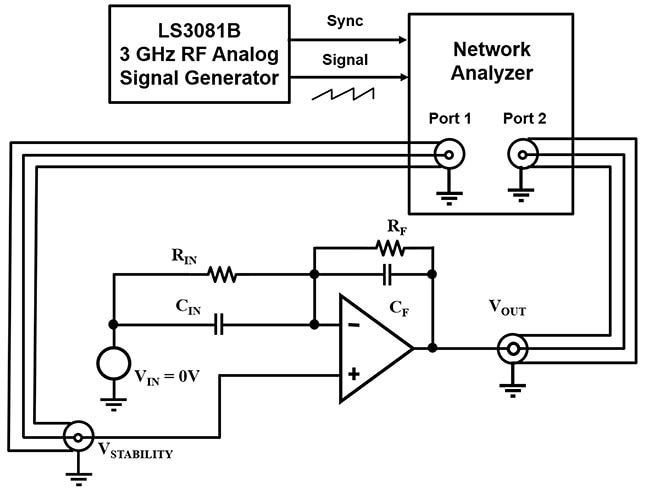Abbildung 9: Konfiguration der Verstärkungs- und Phasenmessung für die invertierende Verstärkerschaltung in Abbildung 5 b.). (Bildquelle: Bonnie Baker)

In Abbildung 9 wird das Eingangssignal des Funktionsgenerators an Port 1 an den Knoten V_STABILITY angelegt. Das Signal breitet sich durch die Verstärkerschaltung zum Ausgang (V_OUT) der Schaltung aus, wo der Netzwerkanalysator das Signal an Anschluss 2 erfasst und mit dem Signal an Anschluss 1 des Funktionsgenerators vergleicht.

Fazit

Wenn es um den Entwurf stabiler Operationsverstärkerschaltungen geht, ist das Bode-Diagramm ein äußerst nützliches Werkzeug, das Sie in Ihre Ausrüstung aufnehmen sollten. Die Leistungsfähigkeit des Bode-Diagramms wird deutlich, wenn Sie sich mit mehrpoligen Schaltungen mit mehreren Nullstellen befassen, bei denen die Schließrate zwischen der Verstärkung bei offener Regelschleife und dem Rückkopplungsnetzwerk schnell die Stabilität Ihrer Schaltung bestimmt.

Dieser Blog kann zwar dabei helfen, die Verwendung des Bode-Plots zu beherrschen, indem er die einfache Verwendung eines Lineals auf Millimeterpapier zeigt, um die Verstärkung im Verhältnis zur Phase einer Schaltung mit Pol und Nullstelle erster Ordnung abzuschätzen, aber der beste Weg zum Lernen ist die Praxis. Denken Sie daran, dass Sie diese Technik üben können, indem Sie eine druckbare Version eines Bode-Diagramms aus den Ressourcen im Online-Handbuch für Innovationen von DigiKey herunterladen.