Come misurare in modo rapido e semplice la risposta in frequenza con un oscilloscopio

Avete bisogno di controllare la risposta in frequenza di un filtro o di misurare la larghezza di banda di un amplificatore? Non è necessario portarsi dietro un analizzatore della risposta in frequenza o di rete. Potete effettuare questa misurazione con un oscilloscopio e un'onda quadra con un fronte veloce.

Le misurazioni della risposta in frequenza richiedono un ingresso con un'ampiezza costante nel campo di frequenza della misurazione. I tre tipi di segnali con uno spettro di frequenza piatto sono il rumore a sweep sinusoidale, impulsivo e in banda larga. Dei tre, la risposta all'impulso produce il risultato più veloce. Quindi la domanda successiva è: come si ottiene una forma d'onda impulsiva?

Ricordate i fondamenti dell'analisi circuitale: l'impulso è la derivata della funzione a gradino. Se si ha la risposta al gradino del dispositivo che si sta testando, la si può convertire nella risposta all'impulso differenziandola. La maggior parte degli oscilloscopi da banco include l'integrazione e la differenziazione come parte dei pacchetti di funzioni matematiche. In questo esempio, è utilizzato l'oscilloscopio HDO 4054A a 500 MHz di Teledyne LeCroy. Per mantenere gli errori di ampiezza sistematici al di sotto di mezzo decibel, la larghezza di banda dell'oscilloscopio deve superare di cinque volte quella del dispositivo misurato. Un oscilloscopio alternativo è WAVESURFER-3054Z di Teledyne LeCroy.

Come si ottiene una funzione a gradino? È facile. Il fronte di salita o di discesa isolato di un'onda quadra o di un impulso è una funzione a gradino. Differenziando la funzione a gradino si produce un impulso. Questo viene illustrato nella Figura 1 per il fronte di salita di un'onda quadra di 10 kHz (traccia superiore).

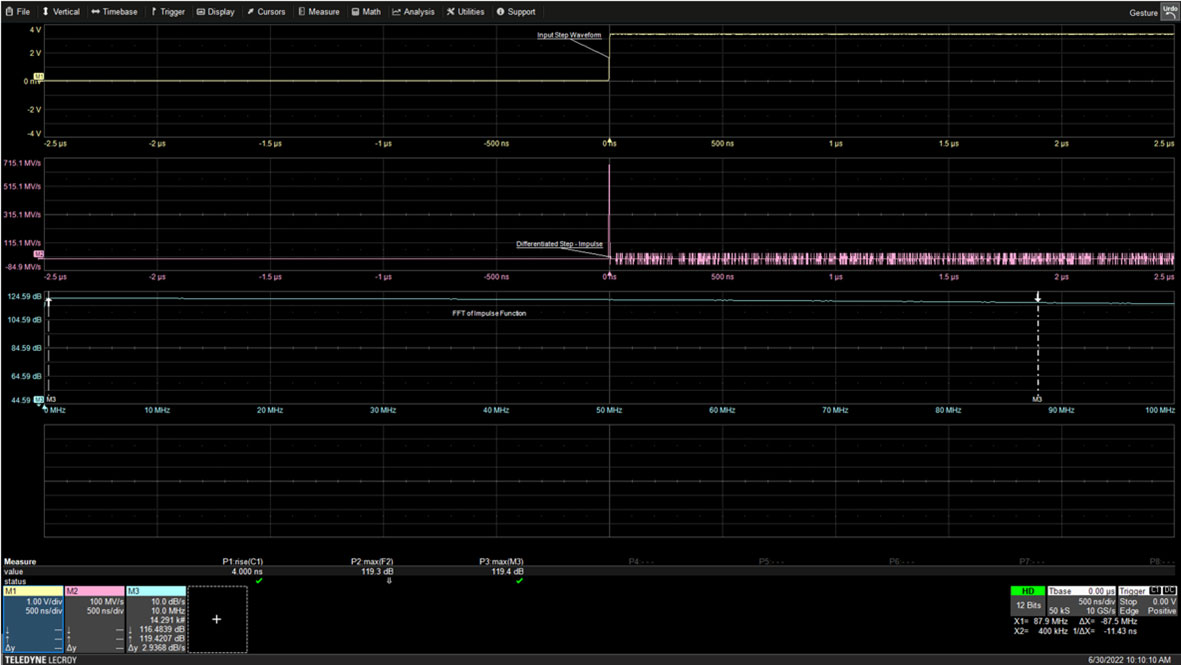Figura 1: Il fronte di salita di un'onda quadra di 10 kHz diventa una funzione di impulso quando è differenziato. Lo spettro dell'impulso è piatto con una larghezza di banda inversamente proporzionale al tempo di salita dell'onda quadra. (Immagine per gentile concessione di Art Pini)

L'oscilloscopio acquisisce solo 5 ms sul fronte. Il bilanciamento dell'onda quadra da 100 ms è fuori dallo schermo. La funzione a gradino viene differenziata utilizzando la capacità matematica dell'oscilloscopio e visualizzata come traccia centrale. La trasformata di Fourier veloce (FFT) dell'impulso è mostrata nella traccia inferiore. La larghezza di banda dell'impulso è determinata dal tempo di salita dell'onda quadra. In questo caso, il tempo di salita viene misurato in 4 ns, come mostrato nel parametro di misurazione P1 sotto le griglie della traccia. La larghezza di banda dell'impulso può essere calcolata come 0,35 diviso per il tempo di salita per un oscilloscopio con una risposta in ampiezza unipolare.

In questo caso il risultato è 87,5 MHz, contrassegnato dal cursore a destra della FFT con un valore numerico all'interno della casella di annotazione della traccia matematica M3. L'ampiezza della FFT a 87,5 MHz è di 116,48 dB rispetto all'ampiezza massima della FFT di 119,43 dB, circa -3 dB dalla massima, a conferma della larghezza di banda del segnale.

La sorgente del segnale per la misurazione della risposta in frequenza dovrebbe offrire onde quadre o forme d'onda impulsive sufficientemente veloci da fornire una larghezza di banda di misurazione adeguata. Il fronte di 4 ns utilizzato nella figura è stato generato da un generatore di forme d'onda arbitrarie a 150 MHz T3AWG2152-D di Teledyne LeCroy. Una sorgente di segnale con un tempo di salita ancora maggiore di 2 ns è T3AFG200 di Teledyne LeCroy, un generatore di funzioni arbitrarie a 200 MHz, 2,4 Gsps. Il tempo di salita di 2 ns fornisce una larghezza di banda del segnale di 175 MHz.

Risposta in frequenza di un filtro passa-basso digitale

L'esempio che segue misura la risposta in frequenza di un filtro passa-basso digitale utilizzando l'oscilloscopio HDO4054A e T3AWG2152-D di Teledyne LeCroy (Figura 2). Queste misurazioni del filtro sono visualizzate nella colonna di sinistra delle tracce.

Il segnale a gradino viene applicato all'ingresso del filtro. L'uscita del filtro viene differenziata e visualizzata. Tenere presente che il filtro ha ampliato la risposta all'impulso a causa della sua larghezza di banda limitata. L'uscita del filtro viene applicata alla FFT e ne viene calcolata la media per produrre la risposta in frequenza dell'ampiezza del filtro.

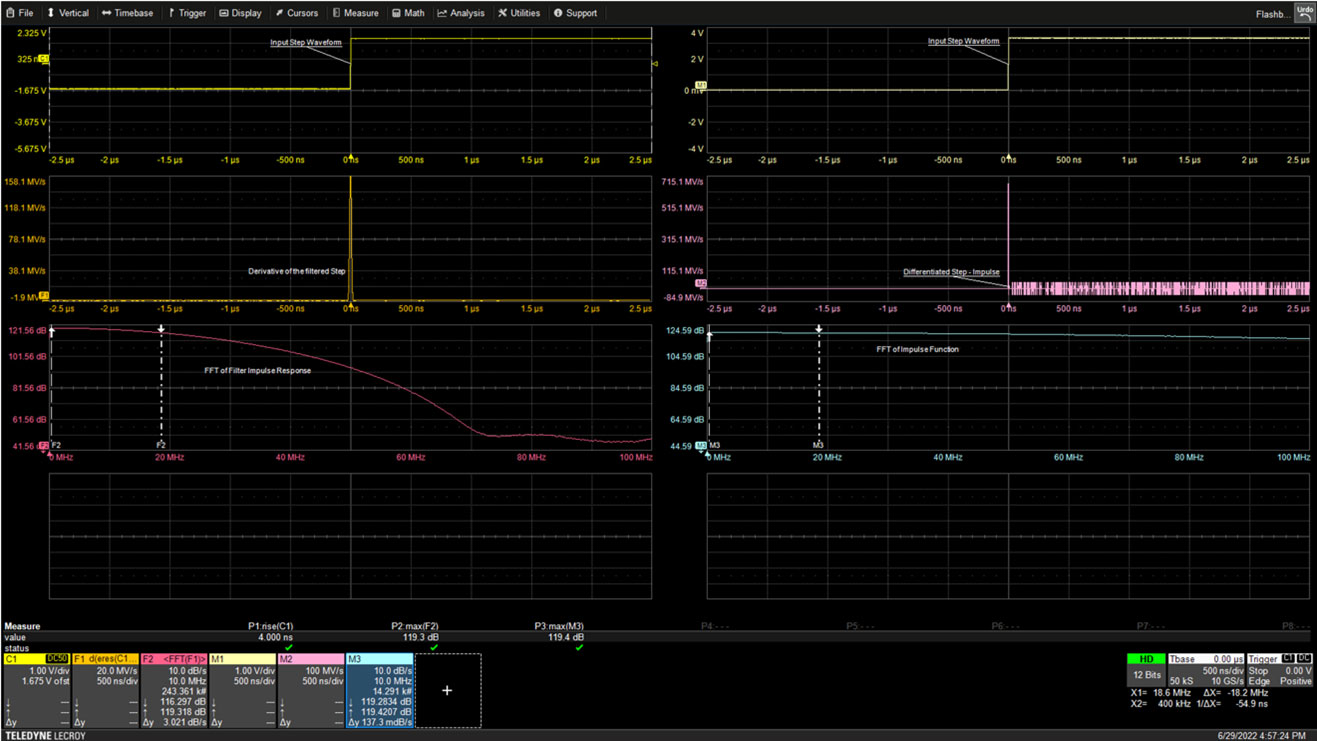Figura 2: Il segnale a gradino, la traccia in alto a sinistra, viene applicato all'ingresso del filtro. L'uscita del filtro viene differenziata e visualizzata nella traccia al centro a sinistra. La FFT del segnale filtrato, traccia in basso a sinistra, mostra la risposta in frequenza del filtro. (Immagine per gentile concessione di Art Pini)

I cursori sulla FFT dell'uscita del filtro leggono la larghezza di banda di -3 dB nella casella di annotazione F2 alla frequenza di 18,6 MHz: questa è la larghezza di banda del filtro. Allo stesso tempo, il cursore sulla FFT della funzione di impulso nella traccia in basso a destra mostra un'attenuazione di soli 0,12 dB nella casella di annotazione M3 a 18,6 MHz, il che indica che la sorgente del segnale è sostanzialmente piatta.

Conclusione

Come mostrato, la risposta dei componenti in funzione della frequenza può essere misurata in modo rapido e facile, senza ricorrere ad analizzatori di rete o della risposta in frequenza, utilizzando le funzioni di base dell'oscilloscopio che operano su un'onda quadra con un fronte veloce.