Principi base del mondo analogico - Parte 2: ADC delta-sigma (ΔƩ): come sfruttarne le capacità digitali

Nota del redattore: I convertitori analogico/digitale (ADC) collegano il mondo analogico a quello digitale e sono quindi fondamentali in qualsiasi sistema elettronico connesso al mondo reale. Svolgono un ruolo determinante anche per le prestazioni di un sistema. Questa serie illustra nei dettagli i fondamenti degli ADC, i vari tipi e le rispettive applicazioni. La Parte 1 di questa serie tratta dei principi base del mondo analogico relativi agli ADC SAR. La Parte 2 prende in esame i convertitori delta-sigma (ΔƩ). La Parte 3 esamina gli ADC pipeline. La Parte 4 mostra come gli ADC delta-sigma possono generare risultati di rumore ultrabasso. La Parte 5 esplora i problemi di pilotaggio dell'ingresso che affliggono gli ADC SAR.

Come si è visto per il convertitore analogico/digitale (ADC) con registro ad approssimazioni successive (SAR) trattato nella Parte 1, la sfida dell'alta precisione di una catena di segnali di sensori analogici - con guadagno multiplo, condizionamento del segnale e complessi stadi di filtraggio analogici, tutti alimentati in un ADC SAR - può portare a passi falsi nel campo analogico. Esiste il rischio che i progettisti finiscano per realizzare una soluzione basata su schede costose e densamente popolate.

Inoltre, a partire dai segnali ultra-bassi dei sensori, l'uscita di ogni stadio analogico della catena di segnali contribuisce a generare errori che si manifestano all'uscita digitale del convertitore sotto forma di un basso rapporto segnale/rumore (SNR) ed errori di distorsione elevata. I progettisti di tali sistemi devono fare un passo indietro e riformulare il paradigma dei sensori ADC ad alta precisione.

La soluzione ai problemi associati a un sistema di sensori ad alta precisione è quella di scegliere una topologia ADC che digitalizzi rapidamente il piccolo segnale del sensore e implementi digitalmente le funzioni analogiche rumorose di guadagno e di filtraggio. Questo è il ruolo dell'ADC delta-sigma (ΔƩ).

Questo articolo descrive brevemente la funzione di base di un ADC ΔƩ e la meccanica interna di conversione analogico/digitale utilizzando come esempio il front-end universale di ingresso analogico/digitale AD4110-1 di Analog Devices. Quindi verrà approfondito l'aspetto della catena di segnali circostante e verranno indicate le specifiche critiche per un sistema di acquisizione dati adeguato.

La struttura di un ADC ΔƩ

Poco prima dell'inizio del secolo, l'ADC ΔƩ ha conquistato il mondo analogico. Con l'adozione diffusa della tecnologia avanzata ΔƩ, il segnale analogico primario e i processi di elaborazione hanno cominciato a prendere campo nel dominio digitale. Esaminando i circuiti integrati (CI) ADC ΔƩ, si nota che oltre l'80% dei dispositivi al silicio svolge funzioni digitali. Il vantaggio del circuito prevalentemente digitale risiede nella robustezza e nell'ingombro ridotto.

Com'è possibile? Si inizia con la digitalizzazione diretta dei segnali analogici a bassa tensione. Una volta nel dominio digitale, i circuiti digitali possono sostituire quasi completamente il filtraggio analogico, svolgendo al tempo stesso tutte le funzioni di guadagno richieste (Figura 1). Inoltre, ad ogni nodo del processo dei semiconduttori, la circuiteria digitale si riduce.

Figura 1: Un ΔƩ contiene quasi tutti i circuiti necessari per il filtraggio e il guadagno. In questo esempio, un ADC ΔƩ rileva e digitalizza la piccola tensione del termometro a resistenza (RTD). Utilizza poi il guadagno e il filtraggio interni del segnale digitale per fornire un risultato digitale a basso rumore a 24 bit. (Immagine per gentile concessione di A Baker’s Dozen)

Nella Figura 1, il sistema ADC ΔƩ a 24 bit è costituito da un ingresso analogico, un motore digitale centrale e un terminale di I/O digitale. Il convertitore acquisisce il segnale dell'RTD a bassa tensione e, attraverso il filtraggio digitale, produce una rappresentazione digitale completa a 24 bit dell'ingresso analogico. In questo caso è assente un blocco di guadagno analogico, che di solito è dominante nei circuiti ADC SAR, e l'unico filtro analogico è la combinazione di R₁ e C₁. Nonostante ciò, si tratta di un filtro di prima classe, semplice ed economico.

Come funziona l'ADC ΔƩ

La topologia di base di un ADC ΔƩ prevede un modulatore ΔƩ in serie con un filtro digitale. Oltre a questa topologia di base, la maggior parte degli ADC ΔƩ ha numerose altre caratteristiche. Tuttavia, tutti i convertitori ΔƩ sono dotati di questo nucleo essenziale (Figura 2).

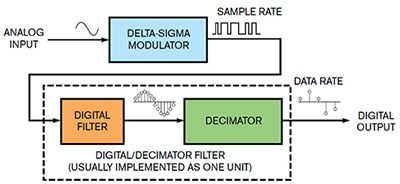Figura 2: Essenzialmente, tutti gli ADC ΔƩ hanno un modulatore ΔƩ, un filtro digitale e un decimatore. (Immagine per gentile concessione di EDN)

Nella Figura 2, l'ingresso può essere sinusoidale o c.c. ma qui tratteremo in particolare dell'ingresso sinusoidale. Il modulatore ΔƩ digitalizza un'onda sinusoidale di un singolo ciclo in un flusso a 1 bit. La frequenza di campionamento in uscita del modulatore ΔƩ è Fs. Sebbene la conversione del modulatore a 1 bit sembri avere un elevato rumore di quantizzazione, il rumore del segnale "prende forma" in realtà nelle frequenze più alte. Questo apre la strada a una conversione a basso rumore e ad alta risoluzione all'uscita del filtro digitale.

All'uscita del modulatore, il filtro digitale accumula i risultati a 1 bit del modulatore ΔƩ ed esegue i calcoli di filtraggio. Il segnale di uscita del filtro digitale riflette digitalmente il segnale analogico in ingresso continuando con una frequenza di uscita Fs. Il segnale ora risiede esclusivamente nel dominio digitale. Un filtro passa-basso digitale, o filtro di decimazione, attenua il rumore a frequenza superiore e rallenta la velocità dei dati in uscita, 1/Fd. Il filtro digitale/decimatore campiona e filtra il flusso di codice a 1 bit del modulatore in un codice multi-bit più lento.

Mentre la maggior parte dei convertitori ha una sola frequenza di campionamento, il convertitore ΔƩ ne ha due: la frequenza di campionamento in ingresso (Fs) e la frequenza dei dati in uscita (Fd). Il rapporto tra queste due variabili di frequenza definisce quello di decimazione del sistema (DR), esemplificato nell'Equazione 1:

Equazione 1

Modulatore ΔƩ

Il modulatore ΔƩ esegue la conversione analogico/digitale effettiva producendo un flusso di codici a 1 bit. Questo processo inizia in un amplificatore differenziale (Figura 3).

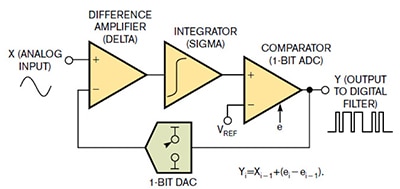Figura 3: Lo stadio di ingresso del modulatore ADC ΔƩ rileva la differenza tra l'ingresso analogico e il DAC di retroazione. Il secondo stadio implementa una funzione di integrazione o sigma sul segnale analogico. (Immagine per gentile concessione di EDN)

Nella Figura 3, l'amplificatore differenziale (delta) trasmette il segnale analogico a un integratore (sigma). All'uscita dell'integratore, un comparatore effettua una discriminazione a una frequenza di campionamento molto alta (1/Fs) tra l'uscita dell'integratore e un riferimento di tensione (V_REF). Inoltre, il comparatore presenta il flusso a 1 bit al convertitore digitale/analogico (DAC) a 1 bit. Il modulatore misura quindi la differenza tra il segnale di ingresso analogico e l'uscita analogica del DAC di retroazione.

Il modulatore ΔƩ modella il rumore verso le frequenze più alte grazie all'azione dell'integratore e dell'anello di retroazione del DAC. La formula nella Figura 3 (in basso a destra) mostra l'equazione di trasferimento come Y_i = X_i-1 + (e_i – e_i-1). Il modulatore digitalizza il segnale di ingresso (X_i) in un codice di uscita a 1 bit (Y_i) con un rumore di quantizzazione (e_i). Nello specifico, l'uscita del modulatore (Y_i) è uguale all'ingresso (X_i-1) più il rumore di quantizzazione (e_i – e_i-1). La formula mostra il rumore di quantizzazione come differenza tra l'errore corrente (e_i) meno l'errore precedente del modulatore (e_i-1).

Filtri digitali e filtri di decimazione

Il calcolo della media è una forma di filtraggio digitale, comune negli ADC industriali a bassa velocità ΔƩ. Quasi tutti gli ADC industriali ΔƩ incorporano la classe dei filtri a media (detti filtri sinc) che utilizzano una risposta all'impulso finita (FIR) a fase lineare, ovvero un filtro passa-basso digitale (Figura 4).

Figure 4: Coefficienti (b_x) in questo filtro a media digitale FIR tutti uguali a uno. (Immagine per gentile concessione di DigiKey)

Nella Figura 4, il bitstream di uscita del modulatore è l'ingresso a questo filtro digitale e il clock di campionamento del modulatore determina il tempo di ritardo. I coefficienti della Figura 4 (b_x) per i filtri FIR sono tutti uguali a uno. Con questo algoritmo di calcolo della media, il filtro digitale FIR genera una rappresentazione digitale a basso rumore, a 24 bit, dell'ingresso analogico come rappresentato nella Figura 3, con campioni che si producono alla frequenza di campionamento del modulatore (1/Fs). Il filtro di decimazione riduce quindi la velocità dei dati in uscita, utilizzando il DR.

Nella sua accezione originale, la decimazione era uno strumento estremo di disciplina militare dell'antica Roma per punire ammutinamenti o atti di codardia, uccidendo un soldato ogni dieci. Nell'elettronica digitale viene applicato lo stesso concetto per ridurre la velocità dei dati di uscita del segnale digitale (1/Fd) del DR. Il modo rapido e digitale per farlo è quello di scartare sistematicamente alcuni dei campioni in uscita del filtro digitale (Figura 5).

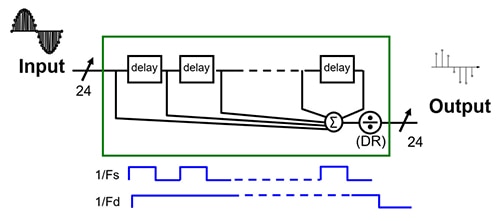Figura 5: Il processo di decimazione riduce sistematicamente il numero di uscite digitali a 24 bit di un fattore della velocità dei dati in uscita (1/Fd, in fondo all'immagine) diviso per la velocità di campionamento (1/Fs). (Immagine per gentile concessione di DigiKey)

Il processo di decimazione nella Figura 5 decima la velocità dei dati in uscita (1/Fd) per il DR, come evidenziato nell'Equazione 1.

Gli eventi attraverso il filtro digitale e di decimazione riducono efficacemente il rumore dell'ADC ΔƩ (Figura 6).

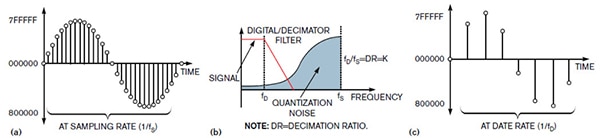Figura 6: Qui vengono mostrati l'uscita digitale del filtro (a) nel dominio del tempo, l'uscita del modulatore formata sul rumore sovrapposta alla funzione passa-basso del filtro di decimazione (b) e il segnale di uscita del decimatore nel dominio del tempo (c). (Immagine per gentile concessione di EDN)

La Figura 6 mostra il segnale digitale mentre passa attraverso il filtro digitale/di decimazione. L'uscita del filtro digitale a 24 bit (Figura 6(a)) funziona alla stessa velocità di quella di campionamento del modulatore (1/Fs). Il modulatore ha già modellato il rumore di quantizzazione in frequenze più alte (Figura 6(b)), in modo che il filtro digitale/di decimazione catturi la porzione di frequenza più bassa del segnale di uscita. L'uscita del filtro di decimazione (Figura 6(c)) produce una rappresentazione digitale a frequenza inferiore del segnale analogico originale.

Espansione digitale

L'ADC ΔƩ risiede principalmente nel dominio digitale. Ora si possono aggiungere facilmente stadi di guadagno programmabili digitalmente, sorgenti di corrente, indicatori di segnale di ingresso a circuito chiuso o aperto e varie interfacce di uscita seriale (Figura 7).

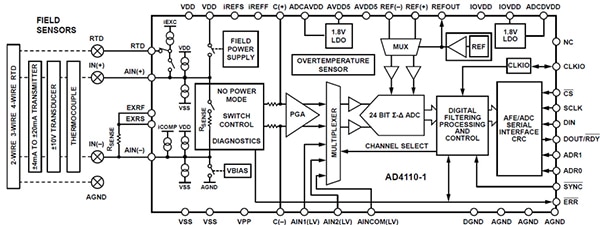Figura 7: AD4110-1 di Analog Devices fornisce numerose funzioni front-end analogiche per sistemi di controllo dei processi industriali. (Immagine per gentile concessione di Analog Devices)

La Figura 7 mostra che l'ADC ΔƩ AD4110-1 di Analog Devices ha numerosi miglioramenti digitali tra cui terminali di ingresso programmabili, funzioni diagnostiche e velocità di trasmissione dati flessibile. Le interfacce dei sensori pronti per l'ingresso includono sensori di temperatura a termocoppia e RTD.

AD4110-1 ha il nucleo di base di un ADC ΔƩ, ma la vocazione digitale del dispositivo consente una serie di funzioni abilitate digitalmente per cui è ora un front-end analogico universale (AFE).

Come per un ADC ΔƩ standard, AD4110-1 è in grado di digitalizzare tensioni estremamente basse da termocoppie, RTD e ponti. Mentre queste funzioni richiedono spesso circuiti di eccitazione aggiuntivi, in AD4110-1 sono integrate.

Per esempio, l'RTD richiede una sorgente di corrente di precisione che sia raziometrica rispetto al riferimento di tensione del convertitore (Figura 8).

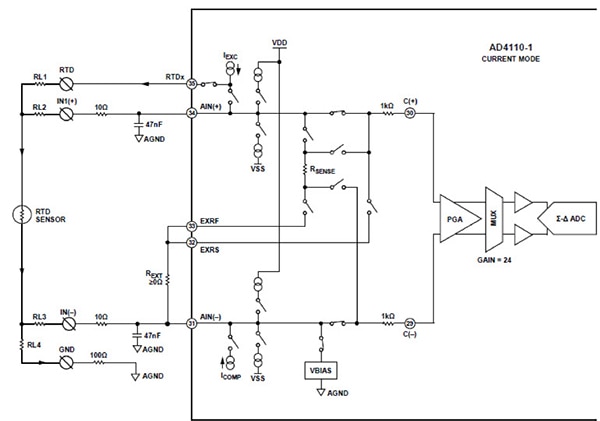Figura 8: Corretto cablaggio di un RTD a quattro fili e dell'ADC ΔƩ AD4110-1. La corrente di eccitazione dell'RTD è programmabile su sei livelli, tra 0,1 mA e 1 mA. (Immagine per gentile concessione di Analog Devices)

Nella Figura 8, AD4110-1 include una corrente di eccitazione che può essere programmata su sei livelli tra 0,1 mA e 1 mA utilizzando il registro del convertitore PGA_RTD_CTRL. La corrente di eccitazione per la resistenza dell'RTD proviene dal pin 35. Il convertitore rileva la caduta di tensione attraverso l'RTD sugli ingressi ad alta impedenza dei pin 34 e 31. L'amplificatore a guadagno programmabile (PGA) AD4110-1 offre 16 guadagni programmabili da 0,2 a 24 V/V. Con questa caratteristica, il progettista è in grado di abbinare ulteriormente il sensore di ingresso all'intervallo di ingresso di AD4110-1. Tra le altre funzioni ausiliarie sono incluse le correnti di pull-up/pull-down per rilevare la presenza di un conduttore aperto (utile con le termocoppie), la calibrazione del guadagno e i coefficienti di correzione.

Conclusione

L'ADC ΔƩ elimina la complessa circuiteria front-end analogica e fornisce un segnale di uscita digitale ad alta risoluzione, con media digitale e a basso rumore, utilizzando un modulatore front-end, un filtro digitale FIR e un filtro di decimazione. Poiché gran parte del circuito è digitale, può essere scalato facilmente con nodi di processo digitali avanzati e si possono aggiungere ulteriori funzionalità mantenendo un ingombro contenuto e una ridotta complessità della scheda.

L'ADC ΔƩ AD4110-1 di Analog Devices sfrutta le caratteristiche di questa architettura ADC. AD4110-1 ha il nucleo di base di un ADC ΔƩ, ma la vocazione digitale del dispositivo consente una serie di funzioni abilitate, tanto che AD4110-1 è ora un AFE universale e realmente pronto per RTD e termocoppie.